What Does Nernst Equation Means?
The Nernst equation offers the connection in between cell potential of the elctrochemical cell, temperature, standard cell potential, and the “Q” reaction quotient.
Surprisingly, taking non-standard conditions under consideration, electrochemical cells’ cell potential can be find out using Nernst Equation.
The “standard cell potential” explains the potential difference that emerges between two half-cells (including concentration of 1M) considering the standard conditions for pressure and the temperature, where pressure is 1 atm and the temperature is 273.15K.
Nevertheless, the cell potential varies with the difference in the concentration, temperature, and pressure. Because it’s responsible for the cell potential change, and the use of Nernst equation is oftentimes used for the calculation of the electrochemical cell’s potential in any condition such as pressure, temperature, and reactant concentration.
Expression
Nernst equation’s expression is expressed as:
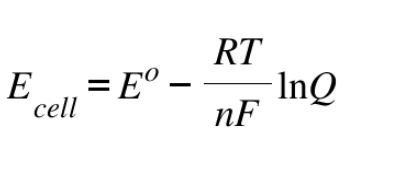
Where,
- E0 = cell potential under the standard conditions
- Ecell = cell’s cell potential
- T = Temperature
- R = The universal gas constant
- n = number of electrons transferred during the Redox Reaction
- Q = Reaction quotient
- F = Faraday constant
According to Nernst Equation, electrochemical cell’s overall potential in a way depends on reaction quotient. Reactants’ consumption and products’ formation over the time duration of reaction which effects cell potential to decrease in a slow manner.
When Nernst reaction reaches the level of chemical equilibrium, then the reaction quotient value is equal to (Kc) equilibrium constant. At this very point, electrochemical cell’s cell potential is having zero value as ΔG = 0 at equilibrium state, in addition to ΔG = -nFEcel.
Derivation
The relation in between (ΔG) change in Gibbs energy plus (Ecell), the cell potential is expressed by following equation.
ΔG = -nFEcell
Under the standard conditions, this very equation is converted into following
ΔG0 = -nFE0cell
The change in Gibbs energy under the non-standard conditions is denoted by the below equation:
ΔG = ΔG0 + RT lnQ
ON substituting these value of ΔG0 and ΔG plus the equation becomes:
-nFEcell = -nFE0cell + RT lnQ
Dividing whole equation by ‘-nF’, and the equation is converted into the following.
Ecell = E0cell – (RT/nF) lnQ
By the conversion of natural logarithm into logarithm of base-10, the equation can be expressed as:
Ecell = E0cell – (2.303RT/nF) logQ
Under standard temperatures where the value of T = 298K, 2.303RT/F value is equal to 0.0592 V.
Substituting 0.0592 V value in earlier equation, the equation can be now represented as:
Ecell = E0cell – (0.0592V/n) logQ
Therefore, electrochemical cell’s Nernst equation is derived.
Determining Equilibrium Constants with the Nernst Equation
Substituting the values of Q and E into the Nernst equation, the following equation is obtained.
When products and reactants of an electrochemical cell attains the equilibrium state, ΔG value becomes zero. So, at this very point, the Kc i.e. equillibrium constant and reaction quotient are same. Because ΔG = -nFE, therefore, cell potential at the equilibrium is zero too.
0 = E0cell – (RT/nF) lnKc
The relationship between equilibrium constant, Nernst equation, and change in Gibbs energy is described below.
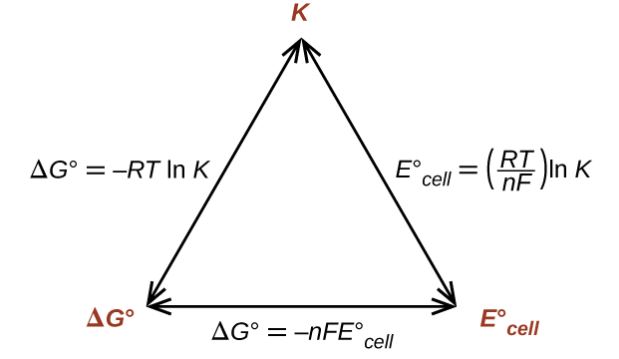
Transforming natural logarithm into logarithm of base-10 plus the substituting of T=298K which is the standard temperature, the equation is converted into following:
E0cell = (0.0592V/n) log Kc
Now, on the rearrangement of this equation, the equation which is obtained is as follows:
log Kc = (nE0cell)/0.0592V
Therefore, equilibrium constant and standard cell potential’s relationship is achieved. When Kc > 1, E0cell value will result in value greater than zero. This indicates that equilibrium prefers forward reaction.
Likewise, when Kc < 1, then E0cell acquires negative value that recommends that reverse reaction is preferred.
Applications of Nernst Equation:
- The Nernst equation’s prime application is to determine the ion concentration.
- Helpful in calculation of ion’s potential having the charge “z” over the membrane.
- The equation is used in marine environment and in oxygen.
- Also, used in pH measurements
- Last, but not least, used in potentiometric titrations and in the solubility products.