De Morgan’s Law refers to the statement that the complement belonging to union of two Sets, Set A and Set B is equal to an intersection of two sets i.e. Set and Set B’s complement. As per De Morgan’s law, also, the intersection of two sets, Set A and Set B’s complement is equal to Union of complement of Set A and Set B, that is,
(A∪B)’ = A’ ∩ B’
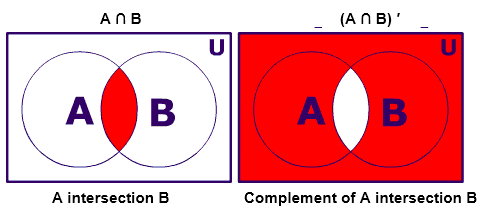
And (A ∩ B)’ = A’ ∪ B’
Set’s complement is described as following:
A’ = { x : x ∈ U & x ∉ A }
Where,
A’ = complement.

Properties of Complement of Sets:
i) Complement Laws: Set A’s Union and its complement, A’ delivers Universal Set U in which, A and A’ are the subset.
A ∪ A’ = U
Also, intersection in Set A in addition to its complement A’ provides the empty set “∅”
A ∩ A’ = ∅
Let’s Say: If U = {1 , 2 , 3 , 4 , 5 } then A = {4 , 5} then, A’ = {1 , 2 , 3 }. From this, you can observe that
A ∪ A’ = U = { 1 , 2 , 3 , 4 , 5}
Also,
A ∩ A’ = ∅
ii) Law of Double Complementation: As per this law, if you take complement of the complemented set A’ then, you’ll have set A itself, as a result.
(A’ )’ = A
In earlier example, you can observe that, if U = {1 , 2 , 3 , 4 , 5} and A = {4 , 5} then A’ = {1 , 2 , 3 }. Now, if you take complement of set A’, you get,
(A’ )’ = {4 , 5} = A
This gives you set A itself.
iii) Law of empty set and universal set:
As per this law, complement of Universal Set contributes in giving an empty set & vice-versa, that is,
∅’ = U And U = ∅’
This law is a self-explanatory one.

Some of the properties of complement sets
(i) A ∪ A’ = A’ ∪ A = ∪ – (Complement law)
(ii) (A ∩ B’) = ϕ – (Complement law)
(iii) (A ∪ B) = A’ ∩ B’ – (De Morgan’s first law)
(iv) (A ∩ B)’ = A’ ∪ B’ – (De Morgan’s second law)
(v) (A’)’ = A (Law of complementation)
(vi) ϕ’ = ∪ (Law of empty set
(vii) ∪’ = ϕ and universal set)
Now,
For any of the two finite sets; Set A and Set B;
(i) (A U B)’ = A’ ∩ B’ (which is De Morgan’s First Law or De Morgan’s Law of Union).
(ii) (A ∩ B)’ = A’ U B’ (which is De Morgan’s Second or De Morgan’s Law of Intersection).
Proof of De Morgan’s law: (A U B)’ = A’ ∩ B’
Assuming:
P = (A U B)’,
Q = A’ ∩ B’,
Let us say that “x” be the arbitrary element of P, subsequently x ∈ P ⇒ x ∈ (A U B)’
– As x ∉ (A U B)
-therefore, x ∉ A and x ∉ B
– And with that, x ∈ A’ and x ∈ B’
– x ∈ A’ ∩ B’ (intersection of sets)
– x ∈ Q
Thus, P ⊂ Q …………….. Equation 1
Furthermore, let y be the arbitrary element of Q, resulting, y ∈ Q ⇒ y ∈ A’ ∩ B’
– y ∉ A and y ∉ B
– y ∉ (A U B)
– y ∈ A’ and y ∈ B’
– y ∈ (A U B)’
– y ∈ P
Accordingly, Q ⊂ P …………….. Equation 2
Now on combining equation 1 and equation 2, what we get is – P = Q, that is, (A U B)’ = A’ ∩ B’
Hence, De Morgan’s First Law gets verified!
Proof of De Morgan’s law: (A ∩ B)’ = A’ U B’
Assuming,
M = (A ∩ B)’,
N = A’ U B’
Taking x as the arbitrary element of M, Next, x ∈ M ⇒ x ∈ (A ∩ B)’
With that:
As, x ∉ (A ∩ B)
So, either x ∉ A or x ∉ B
– When x ∈ A’ or x ∈ B’
– Then, x ∈ A’ U B’
⇒ x ∈ N
Thus, M ⊂ N …………….. Equation 1
In Addition, let y be the arbitrary element of N, then y ∈ N ⇒ y ∈ A’ U B’
– y ∈ A’ or you can say y ∈ B’
– When, y ∉ A or y ∉ B
– Then, y ∉ (A ∩ B) (intersection)
⇒ y ∈ (A ∩ B)’ (complement of intersection)
⇒ y ∈ M
Thus, N ⊂ M …………….. (ii)
Now on combining equation 1 and equation 2, we get – M = , that is, (A ∩ B)’ = A’ U B’
Hence, De Morgan’s Second Law is verified!