one-to-one function
one-to-one function or injective function is one of the most common functions used.
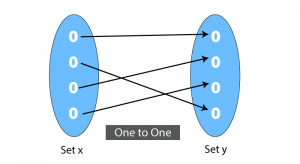
One-to-One functions define that each element of one set say Set (A) is mapped with a unique element of another set, say, Set (B).
To understand this, let us consider ‘f’ is a function whose domain is set A. The function is said to be one to one if for all x and y in A,
x=y if whenever f(x)=f(y)
In the same manner if x ≠ y, then f(x) ≠ f(y)
Formally, it is stated as, if f(x)=f(y) implies x=y, then f is one-to-one mapped or f is 1-1.
if f(x) = y then only f-1(y) = x
Example 1: Show that f: R → R defined as f(a) = 3a3 – 4 is one to one function?
Solution:
Let f (a1) = f ( a2 ) for all a1 , a2 ∈ R
So 3a13 – 4 = 3a23 – 4
a13 = a23
a13 – a23 = 0
(a1 – a2) (a1 + a1a2 + a22) = 0
a1 = a2 and (a12 + a1a2 + a22) = 0
(a12 + a1a2 + a22) = 0 is not considered because there are no real values of a1 and a2.
Therefore, the given function f is one-one.
Onto Function
To explain Onto function consider two sets, Set A and Set B which consist of elements. Ifthere is at least one or more than one element matching with A for every element of B, then the function is said to be onto function or surjective function.
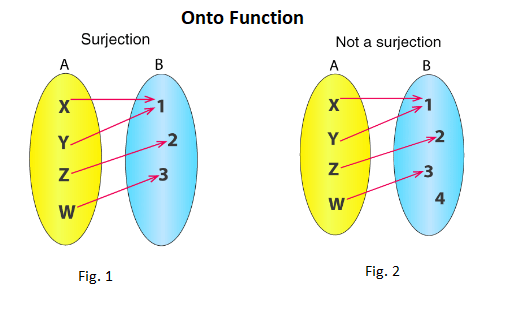
You can see in the figure that for each element of B there is a pre-image or a matching element in Set A. Hence it is called an onto function. In the second figure it can be seen that one element in Set B is not mapped with any of the element of set A. Because of this it’s not an onto function
- Every onto function has a right inverse and every function with a right inverse is an onto function. When we compose onto functions, the result will be onto function only.
Example: Let A={1,5,8,9) and B{2,4} And f={(1,2),(5,4),(8,2),(9,4)}. Then prove f is a onto function.
Solution: From the question itself we get,
A={1,5,8,9)
B{2,4}
& f={(1,2),(5,4),(8,2),(9,4)}
Here, the entire element on B has a domain element on A or we can say element 1 and 8 & 5 and 9 has same range 2 & 4 respectively.
Therefore, f: A → B is ansurjective function.
Hence, the onto function proof is explained.