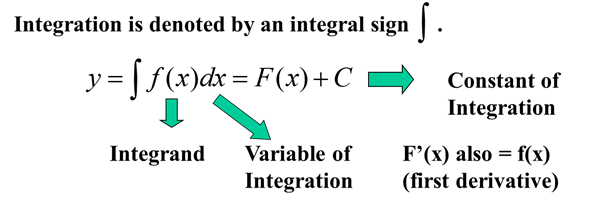
Integration is the process that involves either the evaluation of an indefinite integral or a definite integral. The indefinite integral is a function g with derivative Dx [g(x)] =f(x). Notice that integration is the inverse process of differentiation. Contrary to differentiating a function, we are given the derivative of a function and asked to find its original function. This process is known as integration or antidifferentiation.
Therefore, we can conclude that if f is a function that is continuous on [a, b] then the function g can be defined such that
$g(x)= \int_{a}^{x}{f (t)dt;a\le x\le b}$
Then, $g^{‘}(x)=f(x)$
Also, $\int_{a}^{b}{f (t)dt}=F(b)-F(a)$
In this case, g can be viewed as an anti derivative of f, that is g’(x)=f(x) for a < x < b. This equation interprets that if we first integrate f and then differentiate the result, we get back to the original function f. F also indicates the anti derivative of f, that is, F’ = f. Hence, if we take a function F, first differentiate it, and then integrate the result, we obtain the original function F, but in the form F(b) – F(a).
The definite integral is a number whose value depends on the function f and the numbers a and b, and it is defined as the limit of a riemann sum. Indefinite integral involves an arbitrary constant; for instance,
$\int{x^{2}dx}=x^{3}+c$
The arbitrary constant c is called a constant of integration such that the derivative of a constant is always 0. For integration, there is a possible constant involved, but it is an unknown value unless the lower and higher limit of integration is provided for a particular problem. Therefore, C is used to represent the unknown value.To solve for C, you will be given a problem that gives you the y(0) value. Then you can plug the 0 in for x and the y(0) value for y.
If f(x) = c, where c is a constant, on the interval [a,b], then
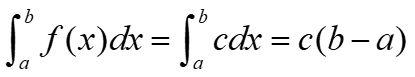
Table of Indefinite Integrals
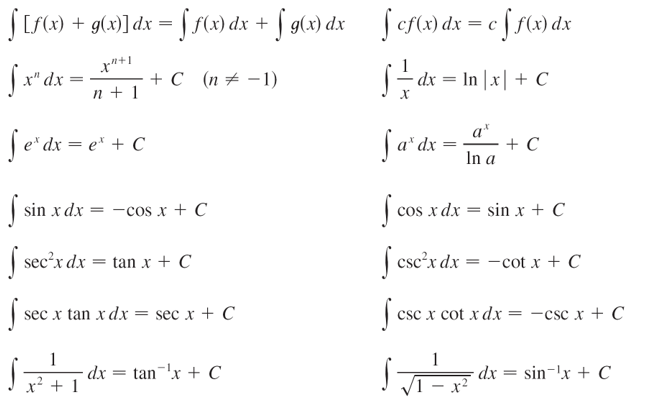
Example find the derivative of the given function: ![]()
Solution:
Since we know that ![]() is a continuous function, we can conclude from the definition of integral that:
is a continuous function, we can conclude from the definition of integral that: ![]()
Example: Find the general indefinite integral (10x4 – 2 sec2x) dx
Solution:
Using our convention and Table 1 and the properties of integrals, we have
(10x4 – 2 sec2x) dx =10 x4dx – 2 sec2x dx
= 10 – 2 tan x + C
= 2x5 – 2 tan x + C