Consider a vector as shown below on the x-y-z plane. The angles made by this line with the +ve direactions of the coordinate axes: θx, θy, and θz are used to find the direction cosines of the line: cos θx, cos θy, and cos θz. Likewise, the direction cosine of θx, θy, and θz in the opposite direction of the line are –cos θx, -cos θy, and -cos θz
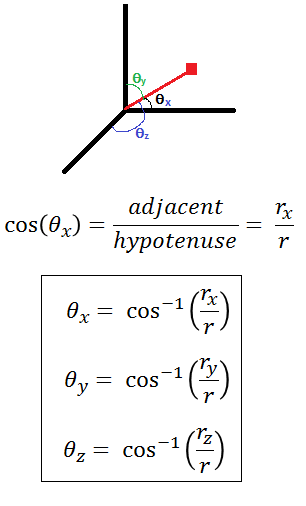
Note that the angles θx, θy, and θz are the direction angles that satisfy the condition: 0<θx, θy,θz<π. Also, the sum of direction angles: θx + θy + θz≠ 2π because these angles do not lie on the same plane.
For a line on the x-axis, the direction cosines are cos 0, cos π/2, cos π/2 = 1, 0, 0.
For a line on the y-axis, the direction cosines are cos π/2, cos 0, cos π/2 = 0, 1, 0.
For a line on the x-axis, the direction cosines are cos π/2, cos π/2,cos 0 =0, 0, 1.
Consider a point P (x, y, z) on a 3D plane such that OP = $\overrightarrow{r}$ and let l, m and n be the direction cosine of $\overrightarrow{r}$ then we can conclude that: x=l$\overrightarrow{r}$, y=m$\overrightarrow{r}$, and z=n$\overrightarrow{r}$.
Hence,
$l=\frac{x}{\overrightarrow{r}}=\frac{x}{\sqrt{x^{2}+y^{2}+z^{2}}}$
$m=\frac{y}{\overrightarrow{r}}=\frac{y}{\sqrt{x^{2}+y^{2}+z^{2}}}$
$n=\frac{z}{\overrightarrow{r}}=\frac{z}{\sqrt{x^{2}+y^{2}+z^{2}}}$
The equation of the line can be written as: $l^{2}+m^{2}+n^{2}=1$
Proof:
We know that l = cosθ$_{x}$, m = cosθ$_{y}$, and n = cosθ$_{z}$
And, cos$^{2}$θ$_{x}$ + cos$^{2}$θ$_{y}$ + cos$^{2}$θ$_{z}$ = 1
cos$^{2}$θ$_{x}$ + cos$^{2}$θ$_{y}$ + cos$^{2}$θ$_{z}$= $(\frac{x}{\overrightarrow{r}})^{2}+(\frac{y}{\overrightarrow{r}})^{2}+(\frac{z}{\overrightarrow{r}})^{2}=\frac{x^{2}+y^{2}+y^{2}}{r^{2}}=\frac{r^{2}}{r^{2}}=1$
Now consider two points in a line segment $\overrightarrow{AB}$, with the coordinates A (x$_{1}$, y$_{1}$, z$_{1}$) and B (x$_{2}$, y$_{2}$, z$_{2}$). Then, their direction cosines can be written a$(\frac{x_{2}-x_{1}}{\overrightarrow{r}}, \frac{y_{2}-y_{1}}{\overrightarrow{r}}, \frac{z_{2}-z_{1}}{\overrightarrow{r}})$.
In this case, $\overrightarrow{\vert r\vert}=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}$
Example: A line makes 30°, 60° and 90° with the x, y and z axes respectively. Find their direction cosines.
Solution:
l = cosθ$_{x}$ = cos 30° = $\frac{\sqrt{3}}{2}$
m = cosθ$_{y}$ = cos 60° = $\frac{1}{2}$
and n = cosθ$_{z}$= cos 90° = 0
The direction cosines are: $(\frac{\sqrt{3}}{2}, \frac{1}{2}, 0)$
Example: Consider a point P $(\sqrt{3},1, 2\sqrt{3} )$ in a 3D space, find the direction cosines of $\overrightarrow{OP}$
Solution: The direction ratios of point P= $(\sqrt{3},1, 2\sqrt{3} )$
Recall that $l=\frac{x}{\overrightarrow{r}}=\frac{x}{\sqrt{x^{2}+y^{2}+z^{2}}}$
$m=\frac{y}{\overrightarrow{r}}=\frac{y}{\sqrt{x^{2}+y^{2}+z^{2}}}$
$n=\frac{z}{\overrightarrow{r}}=\frac{z}{\sqrt{x^{2}+y^{2}+z^{2}}}$
In this case, $\overrightarrow{r}=\overrightarrow{OP}$ and (x, y, z) = $(\sqrt{3},1, 2\sqrt{3} )$
$\vert \overrightarrow{OP}\vert =\sqrt{(\sqrt{3}-0)^{2}+(1-0)^{2}+(2\sqrt{3}-0)^{2}}=\sqrt{3+1+12}=4$
The direction cosine of $\overrightarrow{OP}$ are: $(\frac{\sqrt{3}}{4},\frac{1}{4},\frac{2\sqrt{3}}{4})=(\frac{\sqrt{3}}{4},\frac{1}{4},\frac{\sqrt{3}}{2}
)$