In physics, simple harmonic motion is a distinct type of oscillation. In simple harmonic motion, the restoring force is directly proportional to its displacement and force is applied in the opposite direction to displacement.
An object is experienced simple harmonic motion if;
- The acceleration of an object is directly proportional to the displacement from its equilibrium position
- The direction of acceleration is always toward the equilibrium position
The frequency is several accelerations per second and it is measured in hertz (Hz). The time of one oscillation is called the time and is measured in seconds.
f= 1/T
Acceleration
The acceleration can be calculated at any point of its oscillation by using the equation
In the above equation, the acceleration is measured as, frequency in Hz, and x represents the position from a central point.
Displacement
You must have to calculate the displacement in radians not degrees. We can calculate the displacement of the object from its oscillation position by using the following equation;
![]()
The terms are the same as in the above equation. The additional terms are A which represents the maximum amplitude in m, and t is the time in seconds when oscillation begins.
Velocity
We can calculate the velocity of the object by using the equation below;
![]()
All terms are the same except the v which represents the velocity and measured as.
Simple Harmonic Graph
When we represent the displacement, velocity, and acceleration during the simple harmonic motion against the graph below;
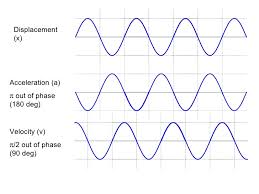
The equation of velocity simplifies the equation of maximum speed and the equation is;
![]()
The equation of maximum acceleration is;
![]()
The time of mass-spring
A mass m is attached to the spring with the constant k which represent the simple harmonic motion
The time of mass-spring is measured by using the equation;
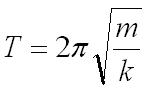
This shows the period of oscillation independent of both amplitude and acceleration.

The time of the pendulum:
The motion of the simple pendulum is approximately equal to simple harmonic motion. The period of mass is attached to the pendulum with the gravitational acceleration g and is given by;
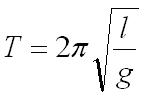
This shows that the period of oscillation is independent of both amplitude and mass but not of acceleration due to gravity.
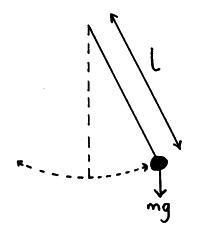
Simple harmonic motion and energy
The pendulum which undergoes simple harmonic motion energy is transferred back and forth between the potential energy and Kinetic energy but the total energy is always the same between the Kinetic energy+ Potential energy.