The progressive wave travels continuously in the medium in the same direction without any change in its amplitude. The progressive wave may be longitudinal or transverse. Let suppose that the plane’s simple harmonic motion is traveling from the O origin along the positive direction in the X-axis. If there is a counting of the time from the instant then the particle at this origin is just passing through the mean position in a positive direction.
In this article, a function will be driven, for describing the propagation of the wave in the medium and to give the shape to the progressive wave at any instant of the time during the propagation. For its understanding, the example of the progressive wave on the string can be considered. Let consider that the y(x, t), is the displacement of the element, at the displacement x and in the time t about the y-axis. By considering the wave, as sinusoidal and periodic, the displacement of the element from the y-axis can be given as follows.
y (x, t ) = a sin (kx – ωt + φ)
This equation can be written as the linear combination, of the cosine and sine function as
y (x, t) =A sin (kx – ωt ) + B cos (kx – ωt )
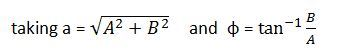
The above equations represent the movement of the transverse waves along the x-axis, where the y(x,t), represents the displacement of the element of the string at position x and at any time interval t, so by using the given time, the shape of the wave can also be determined.
y(x, t) = a sin (kx + ωt + φ ),
By this equation, the negative direction of movement of the wave along the x axis can be determined.
The parameters which are used for the complete description of the harmonic waves are a’, ‘φ’, ‘k’, and ‘ω’. Here the amplitude represents the initial phase change. K is used to denote the angular wavenumber, and ω represents the angular frequency.

The amplitude represents the maximum displacement of the particle, in the wave from a position of equilibrium. The phase describes the state of the motion of the wave. The wavelength has a significant role in the determination of the displacement relation of the wave. It can be defined as the distance over which the shape of the wave is repeated that is analogous to the concept of frequency.