Electrostatic potential at any point of an electric field is defined as potential energy per unit charge at that point.
Electric Potential Energy:
Let us consider a system of two point charges $q$ and $q^{‘}$ (positive test charge) separated by a distance $r$
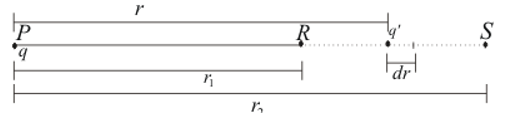
Figure:7.a
Charge $q$ is fixed at point $P$ and is displaced from point R to S along a radial line PRS shown in the figure.
According to Coulomb’s law, the magnitude of the force on a positive test charge as is given by,
![]()
If q’ moves towards $S$ through a small displacement $dr$ then work done by this force is given by,
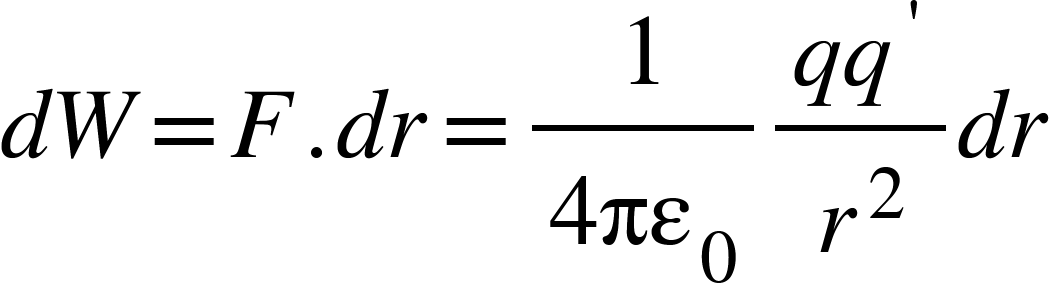
Total work done from point $R$ to $S$ i.e., from $r_{1}$ to $r_{2}$ is given by,
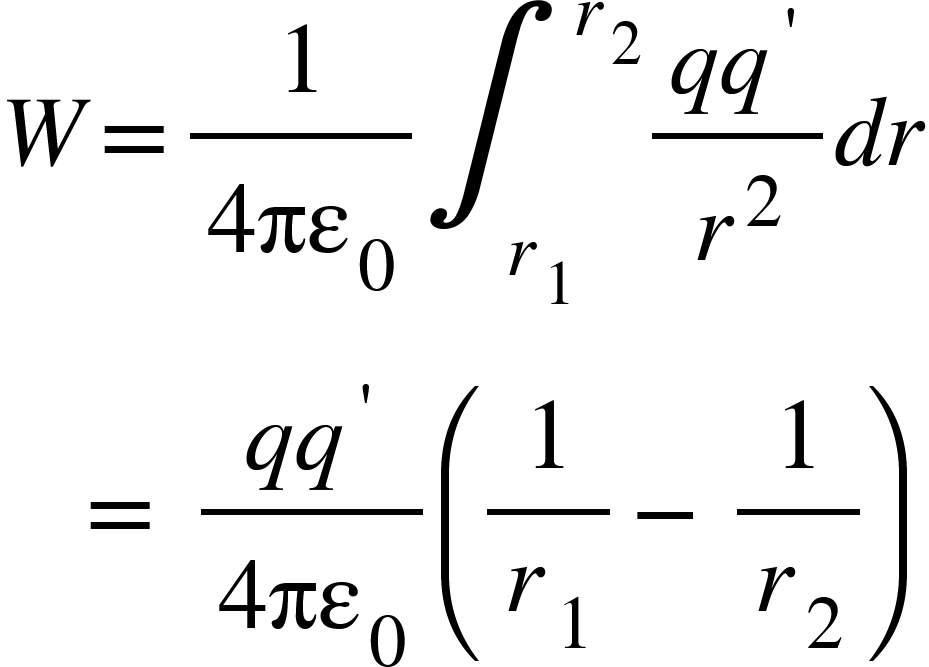
It shows that work done on the test charge depends on end points not on the path taken.
The work done in moving the test charge $q’^{}$ from point $R$ to $S$ is equal to the change in potential energy in moving the test charge $q’^{}$ from point $R$ to $S$.
Thus,
![]()
where
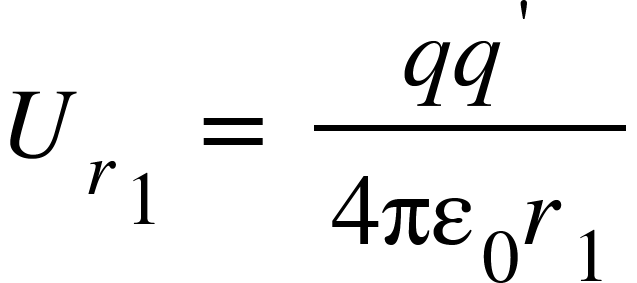
is the potential energy of the test charge $q’^{}$ when it is at point $R$
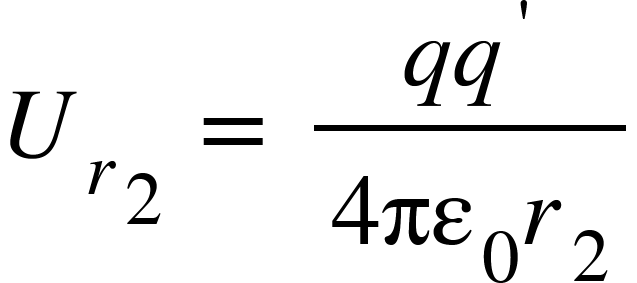
is the potential energy of the test charge $q’^{}$ when it is at point $S$.
Thus potential energy of the test charge $q^{‘}$ at any distance r from charge $q$ is given by
![]()
Electric potential:
Electric potential $V=U/q^{‘}$.
It is a scalar quantity and its SI unit is Volt.
1 Volt = 1 JC$^{-1}$
We have,
![]()
Now dividing both sides of the above equation by $q^{‘}$, we get,
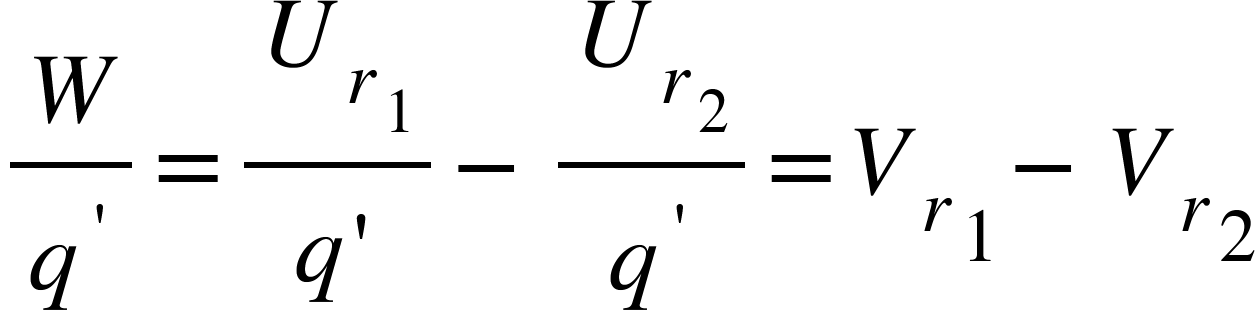
Where $V_{r_{1}}$is the potential energy per unit charge at point $R$ and $V_{r_{2}}$is the potential energy per unit charge at point $S$.
If point $S$ is situated at infinity then,
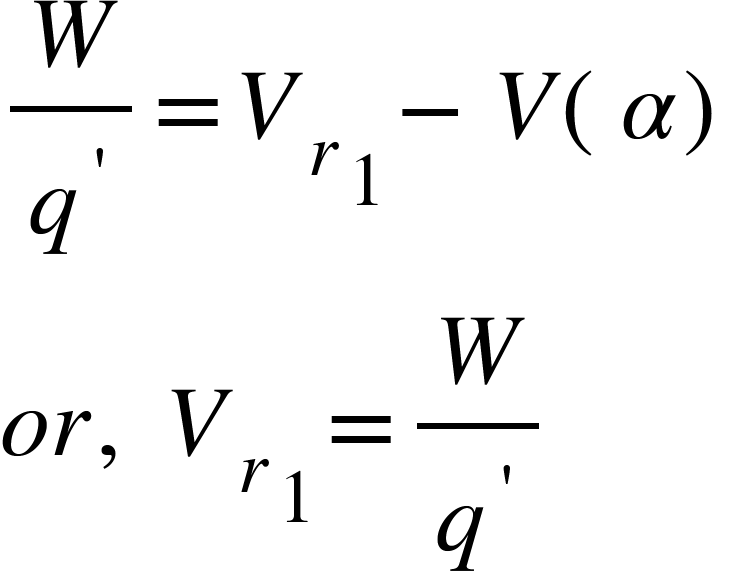
(as Potential energy at infinity is zero)
Therefore, the electric potential at a point in an electric field is the ratio of work done in bringing a test charge from infinity to that point to the magnitude of the test charge.
Potential due to point charge:
We have electric potential at a point due to a test charge $+q$,
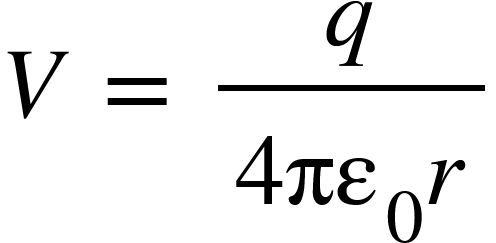
Potential $V$ at any point due to all the point charges in a given system is given by,
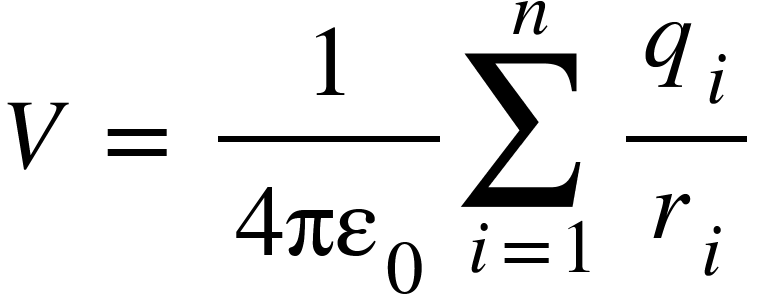
For continuous charge distribution, the above equation becomes,
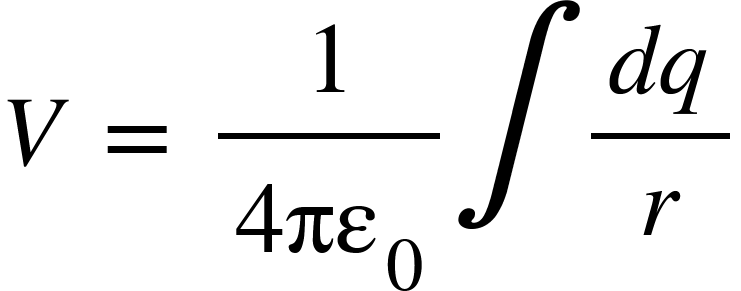
Field and potential gradient:
Let us consider a diagram showing the electric field $E$ due to a point charge $+q$ at point $O in a radially outward direction.
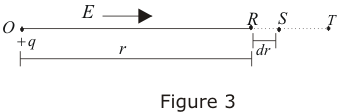
Figure:7.b
Consider a test charge $q^{‘}$is at point R.
Now force on $q^{‘}$ is,
$F=q^{‘}E$
Work done by the force in displacing $q^{‘}$from $R$ to $S$
is,$dW=F.dr=q^{‘}E.dr$
Change in potential energy is,$dU=-dW=-q^{‘}E.dr$
Change in electric potential is,$dV=dU/q^{‘}$
Or, $dV=-E.dr$
Or, $E=-\frac{dV}{dr}$
The quantity $\frac{dV}{dr}$ is the rate of change of potential with distance. This is known as potential gradient.
Negative sign indicates that the potential drops with increasing distance.
A graph of potential gradient and electric field intensity for a radial field is shown below.
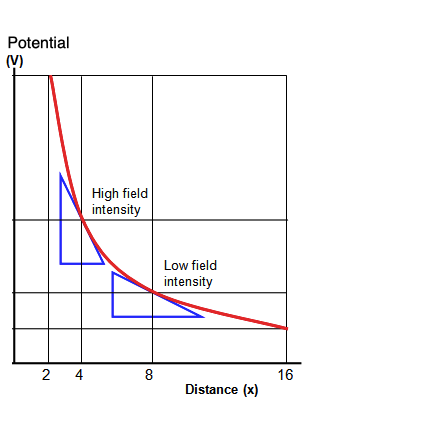
Figure:7.c