Acceleration due to gravity and its variation with altitude and depth
Acceleration due to gravity simply means acceleration gained by an object due to the gravitational force and it has both magnitude and direction that is why it is a vector quantity. Acceleration due to gravity is symbolized by g. Whereas gravity is a force with which earth attracts a body towards its center. The inertial mass and gravitation mass is identical and the precise strength of the earth’s gravity varies depends on the location. The nominal or average value of the earth’s surface is known as standard gravity. Gravity does not normally include the gravitational pull of the moon and sun but they are accounted as a tidal effect.
Variation of g due to latitude
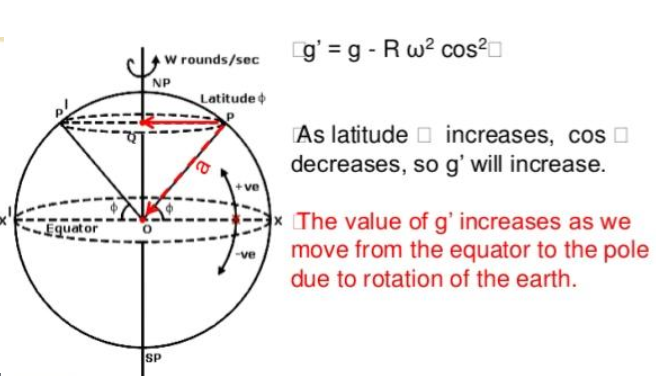
What is the variation in magnitude?
Variation of g due to depth
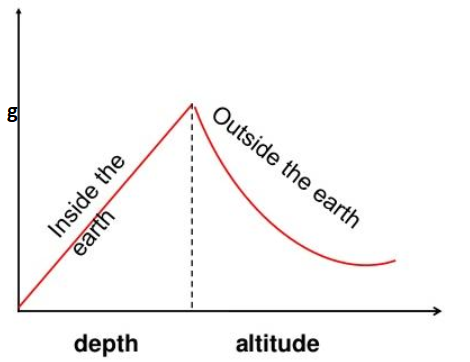
Discussing the altitude and depth of gravitation leads the way as gravity decreases with altitude as one rises above the earth’s surface as greater altitude means more distance from the earth’s surface. There is a huge misconception about astronauts as in orbits they are weightless as they flew high enough to escape earth’s gravity but the altitude of 400 kilometers gravity is still nearly 90 percent as strong as the earth’s surface because of free fall weightlessness occurs. On the other hand, depth is an approximate value for gravity at a distance from the center of the earth and by assuming that the earth’s density is spherically symmetric. There is a consequence that gravity is the same as if all the masses were concentrated at the center. There is a strength of gravity which is reduced by buoyancy forces and the gravitational effects of the moon and the sun which is also known as a tidal effect have a very small effect on the apparent strength of the earth’s gravity.
What is surface acceleration and why lighter objects do not fall faster than heavier objects?
Earth is squashed special instead of exact spherical with the radius at the equator slightly larger than the radius at the poles and this creates a slightly increasing gravitational acceleration at the poles. Also because of centripetal acceleration, the acceleration at the equator is slightly less. And the effect of gravity at the lighter and heavier objects gets bigger and smaller and is equal to the number of times the mass gets bigger or smaller having the ratio remain constant and this concludes that regardless of their mass all freely falling objects accelerate at the same rate.