Recall that a cofactor matrix C of a matrix A is the square matrix of the same order as A in which each element aij is replaced by its cofactor cij .

The adjoint matrix of [A] is written as Adj[A] and it can be obtained by obtaining the transpose of the cofactor matrix of [A]. The minor for element aijof matrix [A] is obtained by removing the ith row and jth column from [A]. We then calculate the determinant of the remaining matrix. The following equation shows the adjoint matrix of A, denoted by adj A, which is the transpose of its cofactor matrix ![]()
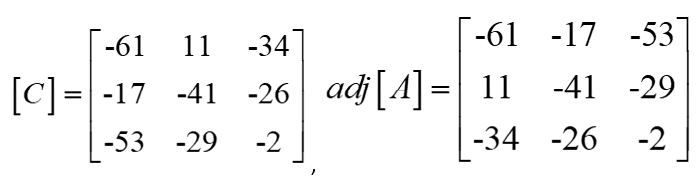
Commutativity can be proven to show that:A(adj A) = (adjA) A = |A| I
Example:
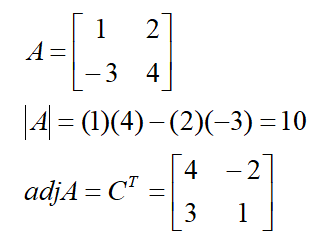
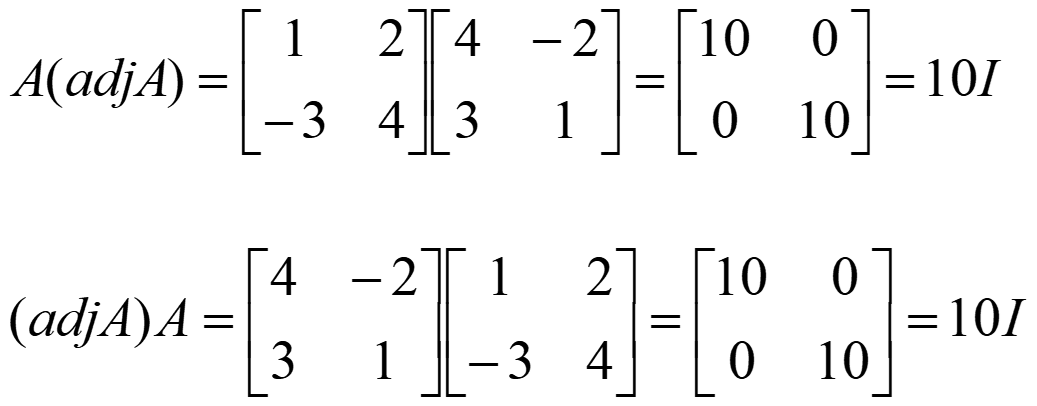
Consider a scalar k. The inverse is the reciprocal or division of 1 by the scalar.
Example:k=7 the inverse of k or k-1 = 1/k = 1/7
Division of matrices cannot defined because in some cases AB = AC while B = C. Instead matrix inversion is used. The inverse of a square matrix, A, if it exists, is the unique matrix A-1,where:AA-1 = A-1A = Iand A(adj A) = (adjA) A = |A| Ithen,
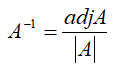
Consider the product A[adj(A)]
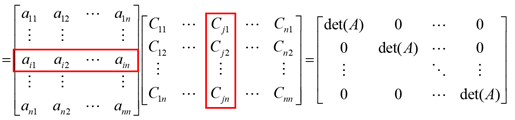
The entry as the position (I, j) of A[adj(A)]
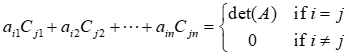
Consider a matrix B similar to matrix A except that the j-th row is replaced by the i-th row of matrix A
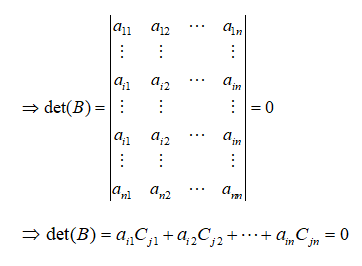
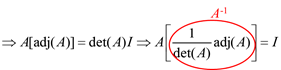
Example: For 2×2 matrix, calculate the inverse:
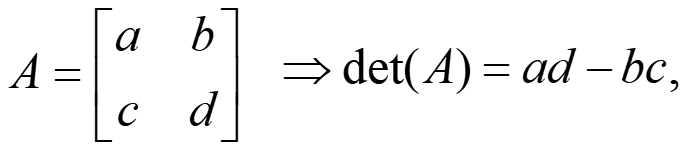
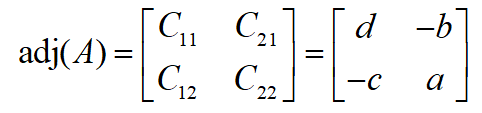
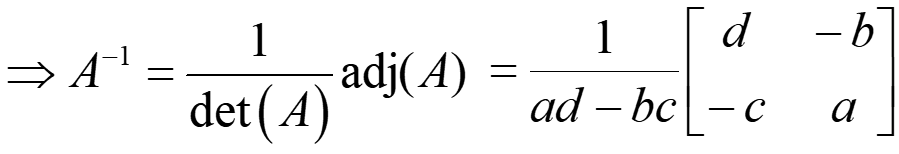
Example:
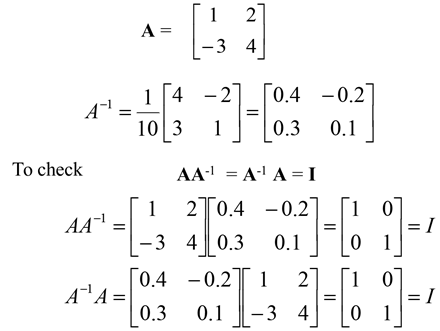
Example:

The result can be verified using AA-1 =A-1A = I. Therefore, the determinant of a matrix must not be zero for the inverse to exist as there will not be a solution. Nonsingular matrices have non-zero determinants and singular matrices have zero determinants
Consider a simple 2 x 2 square matrix:
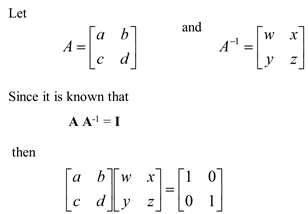
Multiplying gives:
- aw + by = 1
- ax + bz = 0
- cw + dy = 0
- cx + dz = 1
![]()
Therefore,
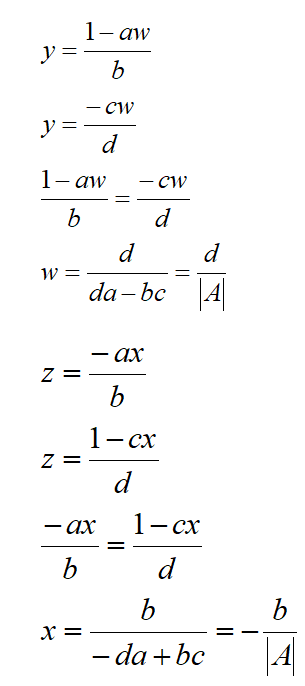
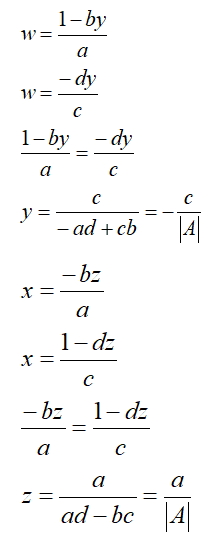
Hence, for 2 x 2 matrix, we can write the inverse as:
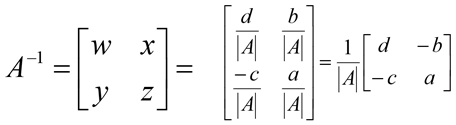
- Exchange elements of main diagonal
- Change sign in elements off main diagonal
- Divide resulting matrix by the determinant