Cartesian equation and vector equation of a line, coplanar and skew lines, the shortest distance between two lines
The vector $\overrightarrow{AB}$ has a definite length while the line AB is a line passing through the points A and B and has infinite length. It can be identified by a linear combination of a position vector and a free vector
In coordinate geometry, the equation of a line is y = mx + c. The equation gives the value (coordinate) of y for any point which lies on the line.The vector equation of a line must show position vector of any point on the line along with a free vector to accommodate all the points in the line.The vector equation of the line through 2 separate fixed points A and B can be written as:

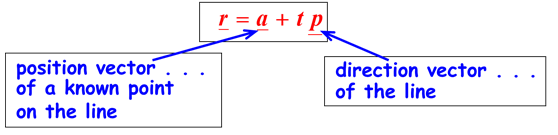
The vector equation of the line through a fixed point A and parallel to the vector p is given by:
Example:
Find the equation of the line passing through the points A and B with position vectors a and b where

Solution:
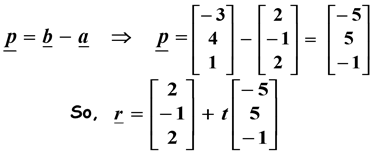
In this example we had:
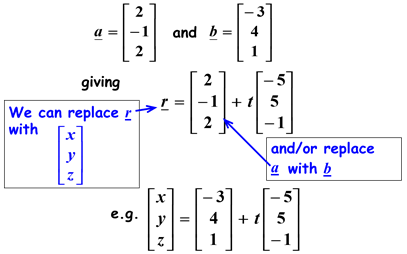
Hence,

However, the value of t for any particular point can be altered because it is a free vector.
The Cartesian equation of a line is given below
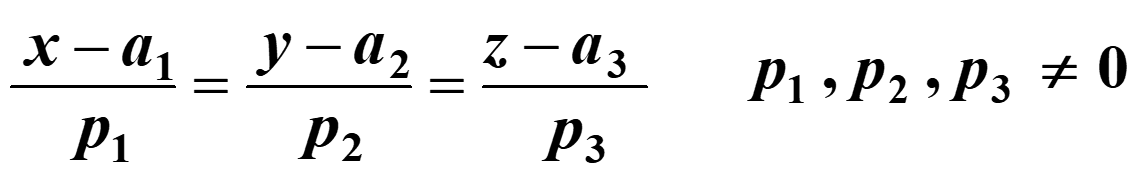
where the position vector of the point on the line is and the direction vector is $\lbrack
\begin{matrix}
a_{1} & \\
a_{2} & \\
a_{3} & \\
\end{matrix}
\rbrack $ and the direction vector is $\lbrack \begin{matrix}
p_{1} & \\
p_{2} & \\
p_{3} & \\
\end{matrix}
\rbrack $
Therefore: Parametric equation can be written as:
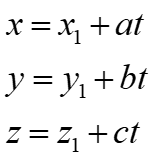
Cartesian equation can be written as:
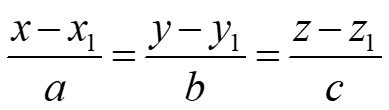
Shortest distance from a point to a line:
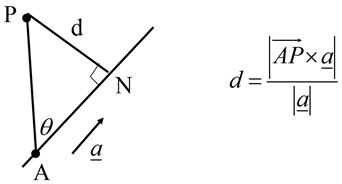
Find the shortest distance between $\overrightarrow{r}=(\begin{matrix}
1 & \\
3 & \\
1 & \\
\end{matrix}
)+\lambda (\begin{matrix}
2 & \\
3 & \\
2 & \\
\end{matrix}
)$ and point P (1,2,3).
(The goal is to find Q first, and then $\vert \overrightarrow{PQ}\vert $)
Point Q is on the line, hence its coordinates must satisfy line equation: $(\begin{matrix}
x_{Q} & \\
y_{Q} & \\
z_{Q} & \\
\end{matrix}
)=(\begin{matrix}
1+2\lambda & \\
3+3\lambda & \\
1+2\lambda & \\
\end{matrix}
)?\overrightarrow{PQ}=(\begin{matrix}
2\lambda & \\
1+3\lambda & \\
-2+2\lambda & \\
\end{matrix}
)$
$(\begin{matrix}
2\lambda & \\
1+3\lambda & \\
-2+2\lambda & \\
\end{matrix}
).(\begin{matrix}
2 & \\
3 & \\
2 & \\
\end{matrix}
)=0$\\
$ . 4\lambda +3+9\lambda -4+4\lambda
=0 ⇒ 17 \lambda =1 ⇒\lambda =\frac{1}{17}$\\
$ ⇒ \overrightarrow{PQ}=(\begin{matrix}
2/17 & \\
20/17 & \\
32/17 & \\
\end{matrix}
) ⇒ find \vert \overrightarrow{PQ}\vert$
In a 3D space, the lines are coplanar when they lie on the same plane and these lines can either be intersecting, parallel or coincident to each other.
Skew Lines are lines that are not parallel but do not meet. They lie in non-parallel planes.
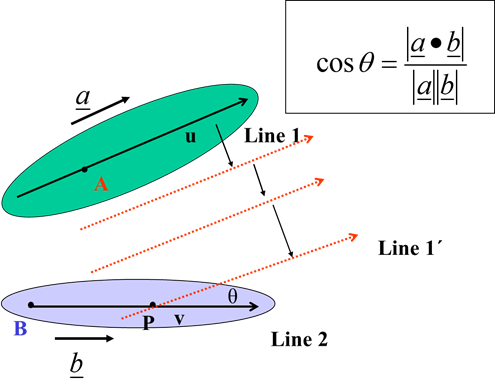
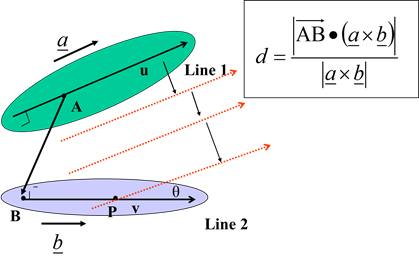
$\overrightarrow{r}=\overrightarrow{a}+\lambda \overrightarrow{b} and \overrightarrow{r}=\overrightarrow{c}+\mu \overrightarrow{d}$can be found as:The cross product of $\overrightarrow{b}$ and $\overrightarrow{d}$ is perpendicular
to both lines, as is the unit vector:${n}=\frac{\overrightarrow{b}\times \overrightarrow{d}}{\vert \overrightarrow{b}\times \overrightarrow{d}\vert }$
The distance between the lines is then $d=\vert {n} .(\overrightarrow{c}-\overrightarrow{a})\vert $
Example:
$\overrightarrow{r_{1}}=\lbrack \begin{matrix}
1 & \\
2 & \\
3 & \\
\end{matrix}
\rbrack +\lambda \lbrack \begin{matrix}
4 & \\
5 & \\
6 & \\
\end{matrix}
\rbrack $ and $\overrightarrow{r_{2}}=\lbrack -\begin{matrix}
1 & \\
2 & \\
-1 & \\
\end{matrix}
\rbrack +\mu \lbrack \begin{matrix}
2 & \\
0 & \\
3 & \\
\end{matrix}
\rbrack $
Are the lines
∙ the same?…….check by inspection
∙ parallel?………check by inspection
skew or do they have one point in common?
$\overrightarrow{r_{1}}=\overrightarrow{r_{2}}$ solving will give 3 equations in and µ.
Solve two of the equations to find two unknowns: and µ.
If we notice that the values of and µ do not satisfy the third equation then it means that the lines are skew which means that they do not intersect each other. It the values obtained to satisfy the three equations then substitute the value of or µ into the appropriate line and find the point of intersection.
Example:
Line 1: $ x=-1+2s, y=1-2s, z=1+4s$
Line 2: $ x=1-t, y=t, z=3-2t$
Line 3: $ x=1+2u, y=-1-u, z=4+3u$
- Show that lines 2 and 3 intersect each other and then find the angle between them
b) Show that line 1 and 3 are skew.
$1-t =1+2u ⇒ t=-2u, t=-1-u ⇒ -2u=-1-u ⇒ u=1 t=-2$
$checking with z: 3-2t=4+3u ?3-2(-2)=4+3(1)$
confirmed intersection $(3, -2, 7)$
direction vectors for line 2 and line 3 are: $\overrightarrow{b}=(\begin{matrix}
-1 & \\
1 & \\
-2 & \\
\end{matrix}
) and \overrightarrow{d}=(\begin{matrix}
2 & \\
-1 & \\
3 & \\
\end{matrix}
)$
$\cos \theta =\frac{\vert \overrightarrow{b} . \overrightarrow{d}\vert }{\vert \overrightarrow{b}\vert \vert \overrightarrow{d}\vert }= \frac{\vert -2-1-6\vert }{\sqrt{1+1+4}\sqrt{4+1+9}}=\frac{9}{\sqrt{84}} ⇒ \theta \approx 10.9^{o}$
b) $-1+2s=1+2u ?2s-2u=2, 1-2s=-1-u ⇒ -2s+u=-2, ⇒ u=0 s=1$
$ checking with z: 1+4s=4+3u ⇒ 1+4(1)=4+3(0) ⇒ 5\ne 4$
⇒no simultaneous solution to all 3 equations.
∴ the line do not meet, and as they are not parallel $(\overrightarrow{b} \ne k\overrightarrow{d} , k\varepsilon R)$ they must be skew.