You may have already known well about what is a Cartesian product of sets. However, here we would consider recalling all of it to reach out better conclusions and discover and learn several more new concepts.
You know that we had earlier talked about defining two non-empty sets A and B that are denoted by AxB and are said to be defined as a collection of ordered pairs (a, b) in a way that a ∈ A and b ∈ B.
A×B = { (a,b):a∈A, b∈B }
When ordered sets are being talked about, it is quite clear that the two elements that would be taken from each set, need to be written down in a particular order. Therefore, if a ≠ b, the ordered pairs (b,a) and (a,b) would be distinct.
Cartesian product of sets of reals (R x R)
Now, consider the following example
A= {a, b, c} ____ (1)
B={x, y} ____ (2)
Then we have,
A×B={(a,x),(a,y),(b,x),(b,y),(c,x),(c,y)} ____ (3)
Make a note of the fact that the first element in each ordered pair is an element of A and the second element in each pair is one from B.
Now, since x ∉ A and a ∉ B; (x,a) ∉ A×B. while it is not really important to consider the order of elements in a set or in the list for the case here; the order of the pairs or the n-tuple is quite important.
For a more geometric interpretation of the Cartesian product of sets of real numbers, consider the below mentioned sets:
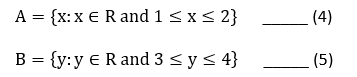
If we consider each of the ordered pairs (x,y) as a point on the Cartesian coordinate system R2 . Then we would have;
![]()
Cartesian product of sets is not only limited to two sets but it could be found for more sets and the complexity tends to increase with the increase in number of sets. While R x R represents the Cartesian product for two sets of real numbers that are represented by R x R; it could be even found for even three sets that would be represented as R x R x R. the above-mentioned example and illustration would help the best to make out and deal with Cartesian products of sets better than ever. You may be able to work along two-dimensional and three-dimensional Cartesian planes accordingly.