Complement of a set

Suppose we have a set A which is a subset of some Universal Set “U”. The complement of A is a set of elements of the Universal Set, which are not the elements of A.

Here, Set A’ complement is estimated w.r.t Universal Set ( Taking everything in mind, Set A refers to a subset of Universal Set, U). This very type of complement is referred to as the Absolute Complement.

If Universal Set is given by U and any subset of U is given by A then A’s complement is the set of all elements of Universal Set “U”, which are not A’s elements.

A′ = { x : x ∈ U and x ∉ A }

As an alternative, it can be mentioned that the difference between subset A and Universal Set U provides us Set A’s complement.

Example

Now, Find complement of Set A and Set B plus the intersection of both complemented sets.

Answer: The Universal Set is determined as:

U = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 }

Also, A = { 2,8,12 }; B = { 7,11,13,15 }

Set A’s complement is described as:

A′ = { x : x ∈ U and x ∉ A }

Hence,

A′ = { 1, 3, 4, 5, 6, 7, 9, 10, 11, 13, 14, 15 }

Similarly, Set B’s complement

B’ = { 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 14,}

The intersection of both sets which are complemented, it’s given by:

A′∩B′⇒ A′∩B′ = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 }

Thus, we can observe that from the above discussions, if a set A is the subset of Universal Set U, then complement of set A, that is, A′ is a subset of U also.

Also, there are different methods for identifying the complement with the use of notation. For example, the main mark can be used. Occasionally, “c”, the lower superscripted case is used.

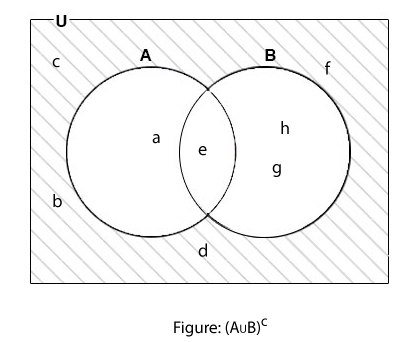
Example: