Introduction to Three–dimensional Geometry: Coordinates of a point
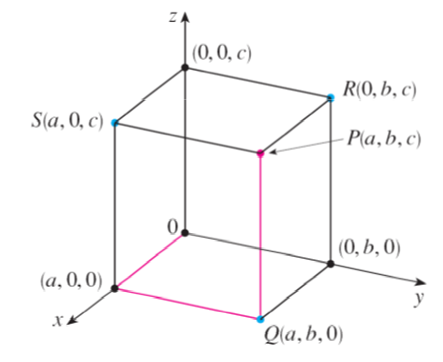
In a 3D plane, assume that P is any point in space. In this place, let a be the (directed) distance from the yz-plane to P, let b be the distance from the xz-plane to P, and let c be the distance from the xy-plane to P. We represent the point P by the ordered triplet (a, b, c), where a,b and c are real numbers. Therefore, a, b, and c are the coordinates of P. Therefore, the location of point P(a, b, c) can be marked by mapping the XYZ octant. For this purpose, we begin at the origin O and move a units along the x-axis, then b units parallel to the y-axis, and then c units parallel to the z-axis as shown in the figure below:
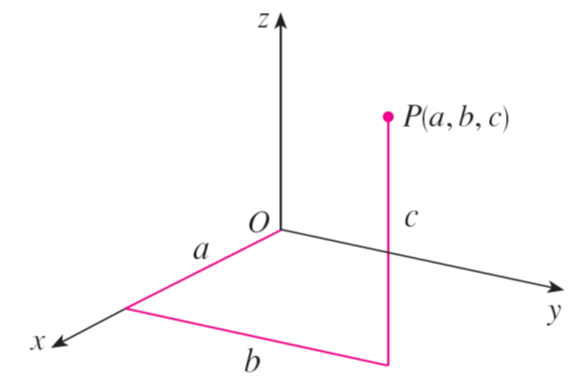
The point P(a, b, c) determines a rectangular box as in the figure below. We start by drawing a perpendicular from P to the xy-plane to get point Q with coordinates (a, b, 0). Point Q is called the projection of P onto the xy-plane. Similarly, R(0, b, c) and S(a, 0, c)are the projections of P onto the yz-plane and xz-plane, respectively as shown in the figure below.
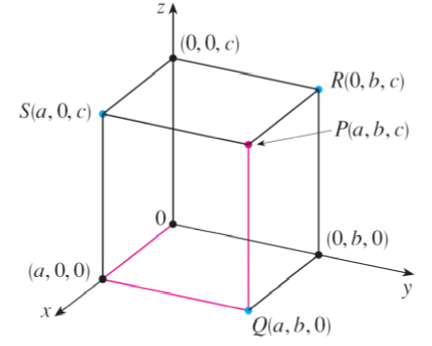
The Cartesian product of R3 = RR R= {(x, y, z) | x, y, z R }has ordered triples of real numbers. We can give an individual correspondence between points P in space and ordered triples (a, b, c) in R3. This formation of this ordered triplet is called a three-dimensional rectangular coordinate system. Here, the first octant can be explained as the set of points whose coordinates are all positive.In 2D analytic geometry, the graph of an equation involving x and y is a curve in R2 while in 3D, an equation in x, y, and z represents a surface in R3.
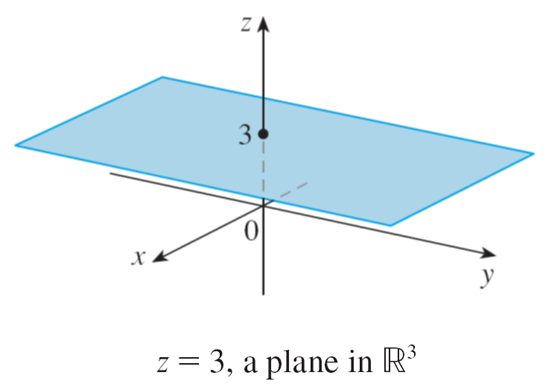
The equation z = 3 represents the set {(x, y, z) | z = 3}, which is the set of all points in R3 whose z-coordinate is 3.In general, if k is a constant, then x = k represents a plane that is parallel to the yz-plane, y = k is a plane parallel to the xz-plane, and z = k is a plane that is parallel to the xy-plane. In the figure below, the faces of the rectangular box are formed by the three coordinate planes x = a, y = b, and z = c and x = 0 in the yz-plane, y = 0 in the xz-plane, and z = 0 in the xy-plane.