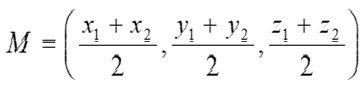Introduction to Three–dimensional Geometry: the distance between two points and the section formula
The familiar formula for the distance between two points in a plane is easily extended from 2D geometry to the following 3D formula.
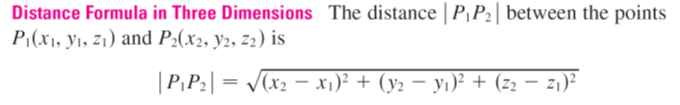
To prove this equation, construct a rectangular box as shown, where: P1 and P2 are opposite vertices.The faces of the box are assumed to be parallel to the coordinate planes.If A(x2, y1, z1) and B(x2, y2, z1) are the vertices of the box, then:
|P1A| = |x2 – x1|
|AB| = |y2 – y1|
|BP2| = |z2 – z1|
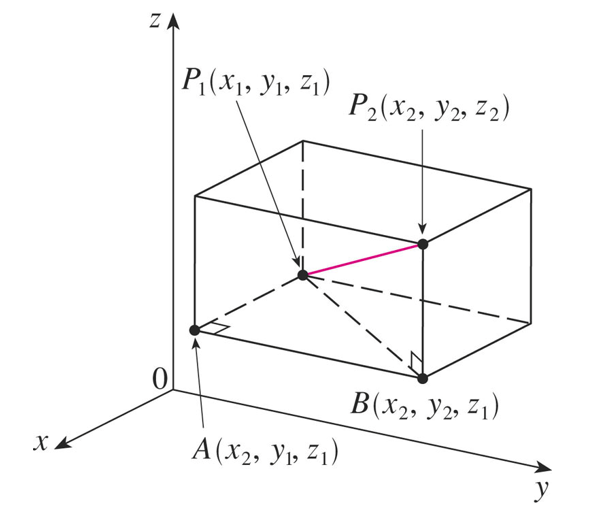
Triangles P1BP2 and P1AB are right-angled.So, two applications of the Pythagorean Theorem give:
|P1P2|2 =|P1B|2 + |BP2|2
|P1B|2 = |P1A|2 + |AB|2
|P1P2|2 = |P1A|2 + |AB|2 + |BP2|2
= |x2 – x1|2 + |y2 – y1|2 + |z2 – z1|2
= (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
Therefore,
![]()
For example, the distance from the point P(2, –1, 7) to the point Q(1, –3, 5) is:
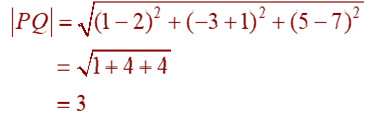
A section is a point that divides a line segment in a given ratio. To evaluate the section formula in the internal or external division for a line in 3D space we consider the following figure:
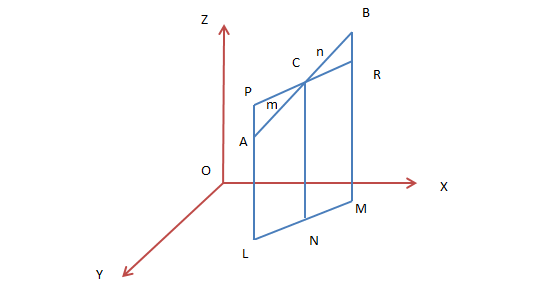
For this purpose, consider two points A (x1, y1, z1) and B(x2, y2, z2) and a point P(x, y, z) dividing AB in the ratio m:n. To find point P, we first draw lines AL, PN, and BM that are perpendicular to XY plane such that AL || PN || BM. This means that the points L, M and N lie on the straight line that is made by the intersection of a plane with AL, PN and BM and XY- plane. From point P, a line segment ST is drawn parallel to LM which intersects AL externally at S and it intersects BM internally at T.Since ST ||LM and AL || PN || BM, the quadrilaterals LNPS and NMTP qualify as a parallelogram. Also, ∆ASP is a similar triangle of ∆BTP therefore,
$\frac{m}{n}=\frac{AP}{BP}=\frac{AS}{BT}=\frac{SL-AL}{BM-TM}=\frac{NP-AL}{BM-PN}=\frac{z-z_{1}}{z_{2}-z}$
Making z as the subject of the equation, we rearrange them to obtain:
mz2 – mz = nz – nz1
mz2 + nz1 = z(n + m)
$z=\frac{mz_{2}+nz_{1}}{m+n}$
Similarly, $x=\frac{mx+nx_{1}}{m+n}$
$y=\frac{my_{2}+ny_{1}}{m+n}$
In conclusion, the coordinates of the point P(x, y, z) that divide the line segment by the points A(x1, y1, z1) and B(x2, y2, z2) in the ratio m:n internally are given by:
$p(x, y,z)=(\frac{mx+nx_{1}}{m+n}, \frac{my_{2}+ny_{1}}{m+n}, \frac{mz_{2}+nz_{1}}{m+n})$
For the case where point P divides the line segment joining the points A(x1, y1, z1) and B(x2, y2, z2) externally in the ratio m:n, then we deduce coordinates of P are by switching n with –n:
$P(x, y,z)=(\frac{mx-nx_{1}}{m-n}, \frac{my_{2}-ny_{1}}{m-n}, \frac{mz_{2}-nz_{1}}{m-n})$
The midpoint M of the line segment PQ with endpointsP(x1, y1, z1 ) and Q(x2, y2, z2 ) is