Definition of Domain
While you may be dealing with relations and functions, you will probably need to understand the concept of domain and range of a relation.
Since the recognition of functions and relations is considered, it would be quite important to make out the domain and range for the same.
What is the domain of function?
The domain for a function or relation is said to be the set of possible inputs for the same. In other words it is the set of considerable input values for which the specific function has been defined. The domain consists of a set of inputs that would suitably be accepted by the function.
For instance, consider the function notation that states, f: R→R f: R→R. This means that f is a function from real numbers to real numbers. In other words, the domain for ff is a set of real numbers RR and its set of possible outputs or codomain is also a set of real numbers (R).
If we have simply defined any function as f(x) = $\sqrt{x-1}$ and do not state its domain explicitly, we would typically have to assume that the domain is then the largest subset of real numbers where the function could be defined. In this example, it could be implicitly understood that the domain is a set of real numbers that are probably equal to or greater than 1: {x | ≥ 1}.
Recognizing the domain
Further, domain could be made out easily from graphical representations and ordered sets also. Having a look at the domain and range of a relation can help in making out whether it is a function or not.
While finding out the domain from ordered sets, take a look at the example mentioned below:
{(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}
Given above is a set of elements. This explains several x’s and y’s and a relation that may be based on those. All the x values here are the domain values and all the y values would s be the range values. The domain and range from the above list could therefore be listed down easily as:
Domain: {2, 3, 4, 6}
Range: {–3, –1, 3, 6}
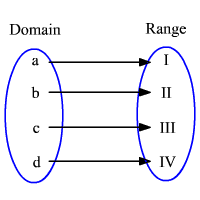
As said before, taking a look at the domain and range of a relation can clarify whether it is a function or not. Each domain value from a relation is supposed to be related to only one value from the ranges set. If there is more than one element from the range set related to any element from the domain set, the relation cannot be called a function.