Electric Field

Let us consider a system, in which a charge $Q$ is placed at the origin and another charge $q$ is placed at a point P. There will be some force of attraction or repulsion between two charges. Now if charge q is removed from the system, there are two possibilities.

1. There is nothing at point P and
2. There is some charge at point P

If we consider there is nothing at point P, then why does the charge q feel a force when again placed at P? This signifies that there is the presence of a force or field which pushes the charge q when placed at P. This proves that there is an electric field produced by the charge Q. Whenever a charge is placed in an electric field; it experiences an electric force on it.

An electric field exists at a point if an electrical force is exerted on a stationary charged object placed at that point.

If $F$is the electric field acting on charge q which is placed at a point in the field, the electric field at that point E = F /q. Clearly, its unit is $NC^{-1}$.

Calculation of electric field:

Let us consider a point P from where a charge $Q$is placed at a distance $r$. If a point charge or test charge $q$is placed at P, then Coulomb’s force is given by,

If the position of charge $q$ is expressed by the vector ${r}$, it experiences a force $F$ equal to the

charge $q$ multiplied by the electric field $E$ at the location of $q.$

Thus, $F(r)=q E(r)$

Direction:

If the electric field is positive, its direction is radially outward. If the field is negative, then its direction is radially inward. The electric field is also called Electric Field Intensity.

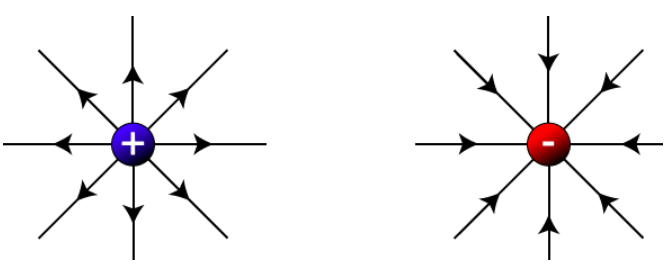
Figure:3.a

Direction of the electric field in case of unit positive charge is shown below.

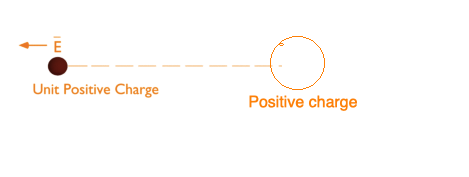
Figure:3.b

Figure:3.c

Electric field due to multiple charges:

Consider a system of charges $q_{1}$, $q_{2}$, ………….$q_{n}$ with position vectors $r_{1}$, $r_{2}$, …………..$r_{n}$

Relative to origin O.

Electric field at a point in space due to the system of charges is defined as the force experienced by a unit test charge placed at that point, without disturbing the original positions of charges $q_{1}$, $q_{2}$……..$q_{n}$

We can use Coulomb’s law and the superposition principle to determine this field at a point P denoted by position vector r.

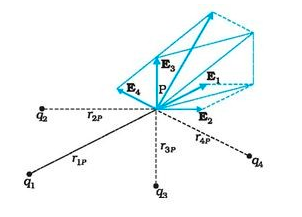
Figure:3.d

Electric field $E_{1}$at point P due to charge $q_{1}$is given by,

Electric field $E_{2}$at point P due to charge $q_{2}$is given by,

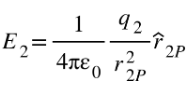
Similarly, electric field $E_{n}$at point P due to charge $q_{n}$ is given by,

By using the principle of superposition, the resultant electric field E will be the vector sum of all the individual electric fields.

Electric Field Lines:

Electric Field Lines show direction of electric field and can be used to describe and interpret the invisible electric field. For example, a charge $q$, is placed at origin. The electric field $E$ produced by charge $q$ can be represented as:

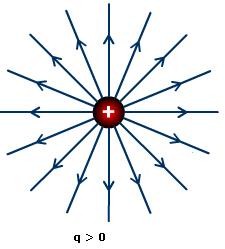
Figure:3.e

The strength of electric fields is directly proportional to the lengths of electric field lines. Also, the strength of the electric field decreases with distance. In case of a positive charge, the direction of arrows points outwards and points inwards in case of a negative charge.

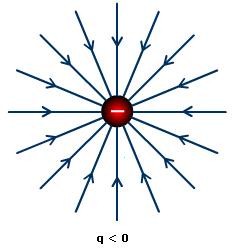
Figure:3.f

Points to remember:

1. Electric field lines never intersect with each other. IIf the electric field lines intersect, then there must be distinctly two electric fields with different directions. This is not possible because for a single location, there is only one direction and magnitude of the electric field associated with it.

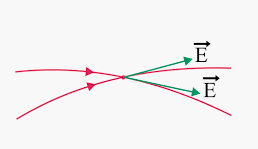
Figure:3.g

2. Electric field lines around a system of two positive charges describe the mutual repulsion between them shown below.

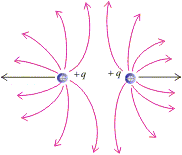
Figure:3.h

3. Electric field lines around a system of one positive charge and another negative charge describe the mutual attraction between them shown below.

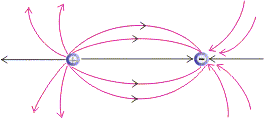
Figure:3.i