Electric Flux:
Electric Flux is defined as a number of electric field lines, passing per unit area.
Consider a plane surface of the area ?S in a uniform electric field E. A positive normal N to the surface makes angle $\theta$ with the electric field E.
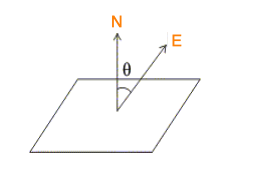
Figure:4.a
Electric flux of the electric field through ?S is given by,$\Delta\phi =E\Delta S cos \theta $
From the above equation, an area vector ΔS of magnitude ΔS can be introduced along the positive normal. Then, $\Delta \phi =E. \Delta S$
The direction of area vector is always along normal to the surface.
If $\theta =90,$then $\Delta \phi =E\Delta S cos 90=0$
The electric flux becomes zero if the normal to the surface is perpendicular to the electric field.
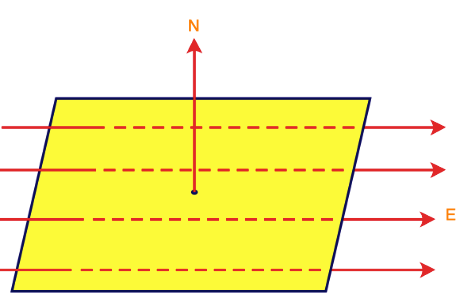
Figure:4.b
Since the strength of electric field is directly proportional to a number of lines passing per unit area, electric flux also signifies for determining the strength of electric field. The S.I unit of electric flux is $Nm^{2}C^{1}$.
Electric dipole:
Electric Dipole is a couple of opposite charges $q$ and $-q$, separated by a distance, say d. The line joining the two charges gives the direction of the electric dipole in space. The direction of the dipole is from negative charge $-q$ to positive charge $q$. The unit of dipole moment is coulomb-meter (Cm).
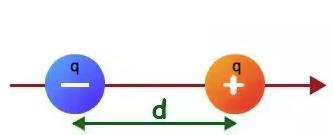
Figure:4.c
The electric dipole is denoted by ${p}$ and equals to the product of the magnitude of charge and distance between the $q$ and $-q$.
![]()
Electric field due to dipole:
Figure:4.d
The electric field due to dipole is called dipole field. The net electric field due to dipole will be the vector sum of the electric field due to charge and .
Electric Field along the axis of the dipole:
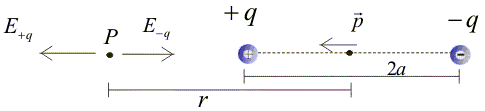
Figure:4.e
Let P be a point at a distance $r$ from the centre of a dipole.
Then electric field due to charge $q$ is given by,
![]()
Electric field due to charge is given by,
![]()
The resultant electric field is given by,
Electric field on the equatorial plane:
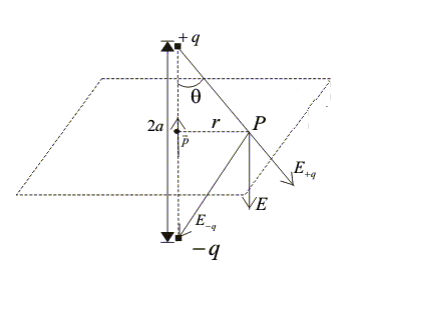
Figure:4.f
From the above figure, Then the magnitude of electric field at P due to charge $q$ and $-q$ is given by,
![]()
and
![]()
From the diagram, it is clear that the vertical component of electric field $E_{1}sin \theta $and $E_{2}sin \theta $will cancel out. Only the horizontal component of field will act and hence, the resultant electric field is given by,
![]()
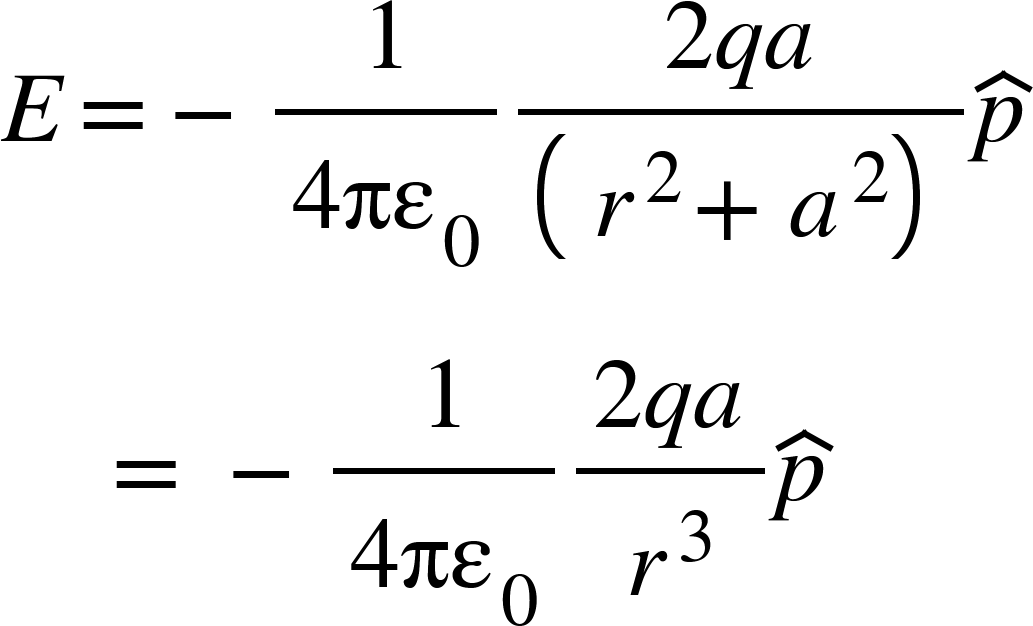
(as $r>>a$)
The above equation shows that dipole depends on the product of $qa$. Hence, the dipole moment vector $p$ of an electric dipole is defined by $p=q\times 2q {p}$.