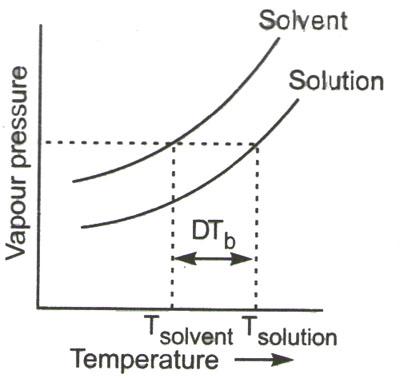
Elevation of boiling point

As known, the liquid only boils when its vapor pressure equals atmospheric pressure. But in case of addition of non-volatile solute to the solvent, the pressure of the vapor is reduced. As to boil the solution, the temperature has to be increased additionally so that its vapor pressure is the same as atmospheric pressure.

The temperature raising is called elevation of boiling point $(\Delta T_b)$ . It’s dependent on the number of moles of the additional solute which is non-volatile in nature.

Thus,

$\Delta T_b \propto m <br> \text{or} \hspace{20mm} \delta T_b = K_b \times m$

The elevation in boiling point here is defined as – T_{b (solution)} – T_{b (pure solvent)}

Here,

= ebullioscopic constant or the constant of molal boiling-point elevation,

‘m’ = molality of a solute.

The calculation can be done – K_b = RT_b²M/ΔH_v,

where R = gas constant,

T_b = boiling temperature of the pure solvent in Kelvins,

M = Molar mass of a solvent

ΔH_v = Enthalpy of vaporization ( ∆H_vap) or heat of vaporization or heat of evaporation per mole of a solvent

Elevation of boiling point

Now, here, Van’t Hoff has co-relation with “ ” along with Enthalpy of vaporization or heat of vaporization, L (expressed in calories/gram of the solvent)

Where T = boiling point of the solvent in Kelvin.

The equation, $\Delta T_b = K_b \times m$ , may be written as:

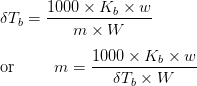
$\delta T_b = \dfrac{1000 \times K_b \times w}{m \times W} <br> \text{or} \hspace{10mm} m = \dfrac{1000 \times K_b \times w}{\delta T_b \times W}$

Where,

w = mass of solute,

W = mass of solvent,

m = molar mass of a solute,

= molal elevation constant

And the $\Delta T_b$ goes up in the boiling point.

Boiling Point Elevation Equation

The amount regarding elevation in boiling point can be estimated by the use of Raoult’s law and Clausius-Clapeyron equation. For the dilute solution which is dilute in nature:

Boiling Point (total) = ΔTb + Boiling Point (solvent)

Where,

ΔTb = molality * Kb * i

Kb = ebullioscopic constant, as mentioned above (0.52°C kg/mol for water) and,

i = Van’t Hoff factor

The ‘i’ factor accounts for individual particles’ number (usually the ions) in a solution, formed by the compound. Examples can be:

- i = 1 in water for sugar
- i = 1.9 in water for sodium chloride, because of nearly full dissociation of a NaCl into Na⁺ and Cl⁻ (generally, simplified as 2)
- i = 2.3 in water for calcium chloride, because of nearly full dissociation of CaCl₂ into Ca²⁺and 2Cl⁻ (generally, simplified as 3)

The factors of Non integer “i” conclude from pairs of ion in solution, that lowers the effective particles’ number present in the solution.

As constant of boiling point elevation is dependent on a solvent. For instance, here are the constants for a few common solvents:

Solvent	Normal Boiling Point, oC	Kb, oC m-1
water	100.0	0.512
benzene	80.1	2.53
chloroform	61.3	3.63
acetic acid	118.1	3.07
nitrobenzene	210.9	5.24