Some improper integrals are discussed below:
$\int{\frac{1}{x}dx=ln\vert x\vert }+C$
$\int{\frac{1}{x^{2}}dx=-\frac{1}{x}}+C$
$\int{\frac{dx}{x^{2}-a^{2}}}=\frac{1}{2a}\log \vert \frac{x-a}{x+a}\vert +c$
Proof: we know that:
$\frac{1}{x^{2}-a^{2}}=\frac{1}{(x+a)(x-a)}=\frac{1}{2a}\lbrack
\frac{(x+a)-(x-a)}{(x+a)(x-a)}\rbrack =\frac{1}{2a}\lbrack
\frac{1}{x-a}-\frac{1}{x+a}\rbrack $
Therefore, $\int{\frac{dx}{x^{2}-a^{2}}}=\frac{1}{2a}\lbrack \int{\frac{1}{x-a}-\int{\frac{1}{x+a}}}\rbrack $
Using the antiderivative of 1/x, we obtain: $\int{\frac{dx}{x^{2}-a^{2}}}=\frac{1}{2a}\lbrack \log \vert x-a\vert \rbrack -\log \vert x+a\vert +C$
$=\frac{1}{2a}\log \vert \frac{x-a}{x+a}\vert +c$
$\int{\frac{dx}{a^{2}-x^{2}}}=\frac{1}{2a}\log \vert \frac{a+x}{a-x}\vert +C$
Proof:
As the above equation, we know that:
$\frac{1}{a^{2}-x^{2}}=\frac{1}{(x+a)(x-a)}=\frac{1}{2a}\lbrack
\frac{(x+a)+(a-x)}{(x+a)(a-x)}\rbrack =\frac{1}{2a}\lbrack
\frac{1}{a-x}-\frac{1}{x+a}\rbrack $
Therefore, $\int{\frac{dx}{a^{2}-x^{2}}}=\frac{1}{2a}\lbrack \int{\frac{1}{a-x}+\int{\frac{1}{x+a}}}\rbrack $
Using the antiderivative of 1/x, we obtain:
$\int{\frac{dx}{x^{2}-a^{2}}}=\frac{1}{2a}\lbrack -loga-x\rbrack +\log \vert x+a\vert +C$
$=\frac{1}{2a}\log \vert \frac{a+x}{a-x}\vert +C$
$\int{\frac{dx}{a^{2}+x^{2}}=\frac{1}{a}\tan ^{-1}\frac{x}{a}+C}$
To prove this integral, we use trigonometric substitution:
Let x = a tan θ, we know that dx = a sec2θdθ
Therefore:
$\int{\frac{dx}{a^{2}+x^{2}}=\int{\frac{a \sec ^{2}\theta d\theta }{a^{2}\tan ^{2}\theta +a^{2}}}}$
$=\frac{1}{a}\int{d\theta }=\frac{\theta }{a}+C=\frac{1}{a}\tan ^{-1}\frac{x}{a}+C$
$\int{\frac{1}{\sqrt{x}}dx}=\int{x^{-\frac{1}{2}}}dx=2x^{\frac{1}{2}}+C$
Specific types of substitutions are recommended when certain radicals appear in an integral.
If $\sqrt{\pm x^{2}\pm a^{2}}$ occurs, we use a trigonometric substitution
If $\sqrt[n]{ax+b}$ occurs, we use the rationalizing substitution. More generally, this sometimes works for $\sqrt[n]{g(x)}$.
$\int{\frac{dx}{\sqrt{x^{2}-a^{2}}}}=\log \vert x+\sqrt{x^{2}-a^{2}}\vert +C$
To prove this integral, we use trigonometric substitution:
Let x = a sec θ, we know that dx = a secθ tanθ dθ
$\int{\frac{dx}{\sqrt{x^{2}-a^{2}}}}=\int{\frac{a sec\theta tan \theta d\theta }{a^{2}\sec ^{2}\theta -a^{2}}}$
$=\int{\sec \theta d\theta =\log \vert \sec \theta +\tan \theta \vert +A}$
$=\log \vert \frac{x}{a}+\sqrt{\frac{x^{2}}{a^{2}}-1}\vert +A$
$=\log \vert x+\sqrt{x^{2}-a^{2}}\vert -log\vert a\vert +A$
$=\log \vert x+\sqrt{x^{2}-a^{2}}\vert +C $
In this case, C = $-log\vert a\vert +A$
$\int{\frac{dx}{\sqrt{a^{2}-x^{2}}}}=\sin ^{-1}\frac{x}{a}+C$
To prove this integral, we use trigonometric substitution:
Let x = a sin θ, we know that dx = a cosθdθ
Hence, we obtain:
$\int{\frac{dx}{\sqrt{a^{2}-x^{2}}}}= \int{\frac{a cos\theta d\theta }{\sqrt{a^{2}-a^{2}\sin ^{2}\theta }}}$
$=\int{d\theta =\theta +C}$
$=\sin ^{-1}\frac{x}{a}+C$
$\int{\frac{dx}{\sqrt{x^{2}+a^{2}}}}=\log \vert x+\sqrt{x^{2}+a^{2}}\vert +C$
To prove this integral, we use trigonometric substitution:
Let x = a tan θ, we know that dx = a sec2θdθ
$\int{\frac{dx}{\sqrt{a^{2}+x^{2}}}}= \int{\frac{a \sec ^{2}\theta d\theta }{\sqrt{a^{2}+a^{2}\tan ^{2}\theta }}}$
$=\int{\sec \theta d\theta =\log \vert \sec \theta +\tan \theta \vert +A}$
$=\log \vert \frac{x}{a}+\sqrt{\frac{x^{2}}{a^{2}}+1}\vert +A$
$=\log \vert x+\sqrt{x^{2}+a^{2}}\vert -log\vert a\vert +A$
$=\log \vert x+\sqrt{x^{2}+a^{2}}\vert +C $
In this case, C = $-log\vert a\vert +A$
To find the integral: $\int{\frac{dx}{ax^{2}+bx+c}}$
We first bring a to the numerator:
$ax^{2}+bx+c=a\lbrack x^{2}+\frac{b}{a}x+\frac{c}{a}\rbrack =a\lbrack (x+\frac{b}{2a})^{2}+(\frac{c}{a}-\frac{b^{2}}{4a^{2}})\rbrack $
Now, put $x+\frac{b}{2a}=t$ such that dx = dt and assuming $\frac{c}{a}-\frac{b^{2}}{4a^{2}}=\pm k^{2}$
The integral form $\frac{1}{a}\int{\frac{dt}{t^{2}\pm k^{2}}}$ depends in the sign of $(\frac{c}{a}-\frac{b^{2}}{4a^{2}})$ which can be evaluated easily.
For finding the integral of type $\int{\frac{px+q}{ax^{2}+bx+c}dx}$, we find real numbers A, B and C such that:
$px+q=A\frac{d}{dx}(ax^{2}+bx+c)+B=A(2ax+b)+B$
To determine A and B, we equate both sides of the coefficients of x and substitute the constant terms. A and B are thus obtained and hence the integral is reduced to one of the known forms
For finding the integral of $\int{\frac{px+q}{\sqrt{ax^{2}+bx+c}}dx}$ we use the same steps as above.
Consider the following examples now:
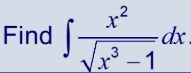
Start by writing
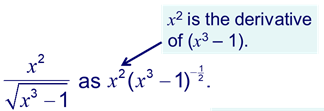
Now consider the derivative of y.
![]()
Using the chain rule:
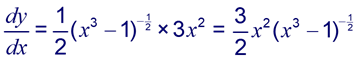
So,
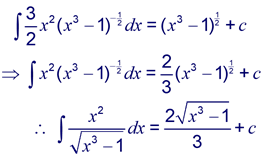
Example:
Remove a factor of 1/5 to write the function in the form f’(x)/f(x)
In general,
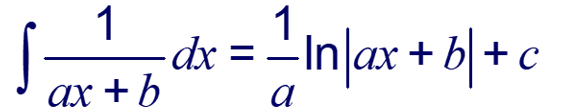
Example: Find the following integral:
$\int{\frac{x+3}{\sqrt{5-4x-x^{2}}}}$
First, we express x + 3 in the form:
$A\frac{d}{dx}(5-4x-x^{2})+B=A(-4-2x)+B$
By equating the coefficient of x and the constant values on both sides, we obtain:
-2a = 1, -4 A + B = 3. Therefore, A = -1/2 and B = 1
$\int{\frac{x+3}{\sqrt{5-4x-x^{2}}}=-\frac{1}{2}\int{\frac{(-4-2x)dx}{\sqrt{5-4x-x^{2}}}}+\int{\frac{dx}{\sqrt{5-4x-x^{2}}}}}$
Now let I$_{1}$=$\int{\frac{(-4-2x)dx}{\sqrt{5-4x-x^{2}}}}$ and I$_{2}$=$\int{\frac{dx}{\sqrt{5-4x-x^{2}}}}$, hence: $\int{\frac{x+3}{\sqrt{5-4x-x^{2}}}=-\frac{1}{2}I_{1}+I_{2}}$
In I$_{1}$, use 5 – 4x – x$^{2}$ = t, such that (- 4 – 2x) dx = dt.
$I_{1}=\int{\frac{(-4-2x)dx}{\sqrt{5-4x-x^{2}}}}=\int{\frac{dt}{\sqrt{t}}}=2\sqrt{t}+C$
$I_{1}=2\sqrt{5 – 4x – x^{2}}+C$
In I$_{2}$, use x +2 =t such that dx = dt
$I_{2}=\int{\frac{dx}{\sqrt{5-4x-x^{2}}}}=\int{\frac{dx}{\sqrt{9-(x+2)^{2}}}=\int{\frac{dx}{\sqrt{3^{2}-t^{2}}}=\sin ^{-1}\frac{t}{3}+D}}$
$=\sin ^{-1}\frac{x+2}{3}+D$
Substituting the values,we obtain:
$\int{\frac{x+3}{\sqrt{5-4x-x^{2}}}=-\frac{1}{2}(2\sqrt{5 – 4x – x^{2}}+C)+\sin ^{-1}\frac{x+2}{3}+D}$
$=-\sqrt{5 – 4x – x^{2}}+sin^{-1}\frac{x+2}{3}+E$
In this case, E = D- C/2