Feasible Solution
A feasible solution for a linear program is a solution that satisfies all constraints that the program is subjected. It does not violate even a single constraint.
Any x = (x1, xn) that satisfies all the constraints.
Example x1 = 5 bowls
x2 = 12 mugs
Z = $40x1 + $50x2 = $700
Labor constraint check:
1(5) + 2(12) = 29< 40 hours, within constraint
Clay constraint check:
4(5) + 3(12) = 56< 120 pounds, within constraint
This LP has a feasible solution
Infeasible Solution
Alternatively, an LP is infeasible if there exist no solution that satisfies all of the constraints. Hence, if no feasible solution can be constructed, then the LP is infeasible. Note that a real operation must remain within the constraints of reality; hence, infeasibility most often indicates an error of some kind. It may stem from an error in specifying some of the constraints or wrong numbers in the data.
For any linear program in standard form: if there is no optimal solution, then the problem is either infeasible or unbounded. If a feasible solution exists, consequently a basic feasible solution also exists. In the presence of an optimum solution, there exists a basic feasible solution that is also an optimum solution.
An infeasible solution violates at least one of the constraints of the LP problem:
Example x1 = 10 bowls
X2 = 22 mugs
Z = $1400
Labor constraint check:
1(10) + 2(22) = 54> 40 hours, violates the constraint
Example:
min: x + y;
c1: x ≥ 6;
c2: y ≥ 6;
c3: x + y ≤ 11;
This model is clearly infeasible.
Example:
Maximize Z = x
Subject to the constraints:
x ≤ −1
x ≥ 0
This model is also infeasible.
Now consider the following example:
Solve the following linear programming problem using the graphical expression:
Maximise Z = 4x + y
Subject to:
x + y ≤ 50
3x + y ≤ 90
x ≥ 0, y ≥ 0
Solution: The shaded region in the figure below is the feasible region determined by the system of constraints (2) to (4). The feasible region OABC is bounded as shown in the graph below. Hence,we can use the Corner Point Method to determine the maximum value of Z.
| Corner Point | Corresponding value of Z |
| (0, 0) | 0 |
| (30, 0) | 120 Maximum |
| (20, 30) | 110 |
| (0, 50) | 50 |
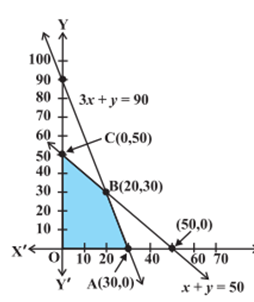
Hence, the maximum value of Z falls at 120 at the point (30, 0) as obtained by the corner point method.