Lets us express the force between two point charges in terms of their position vector.
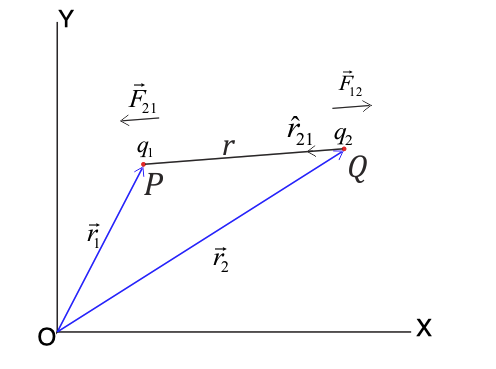
Figure:2.a
Consider two point charges $q_{1}$and $q_{2}$are at P and Q respectively. The position vector of point P is = 
and that of point Q is 
.
Let $r$ be the distance between these charges.
We have,
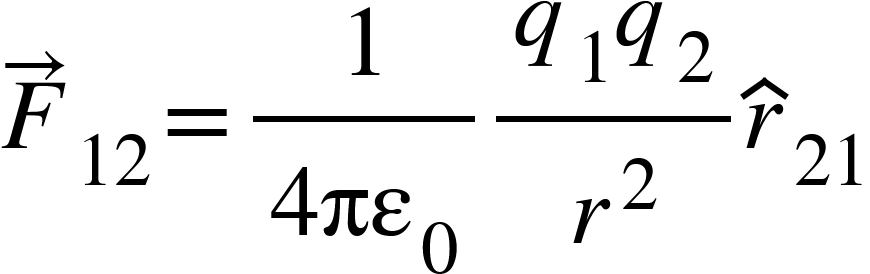
Where 
is the unit vector in direction from $q_{2}$ to $q_{1}$.
The above equation can be rewritten as,
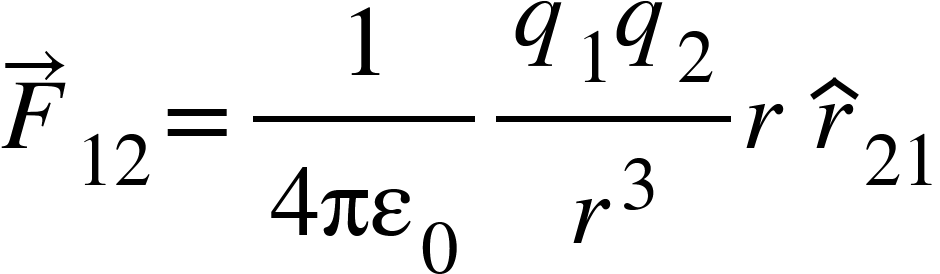……………….. (1)
Using triangle law of vector addition, we have,
And 
Putting these values in equation (1),
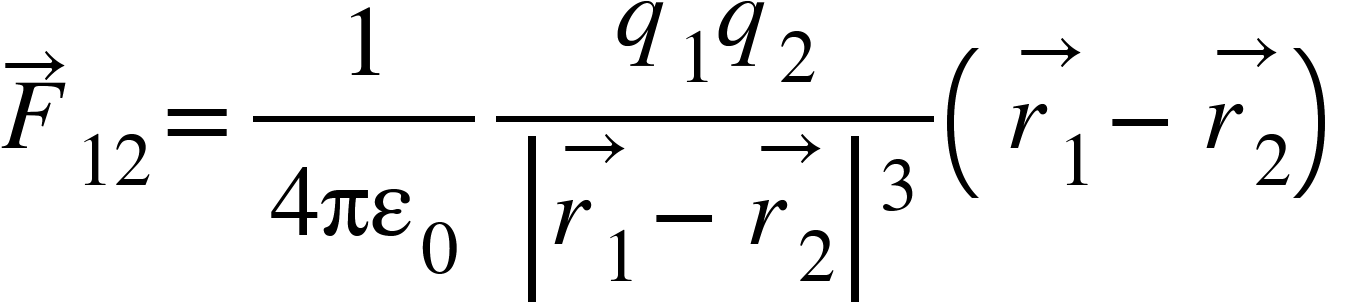
Similarly,
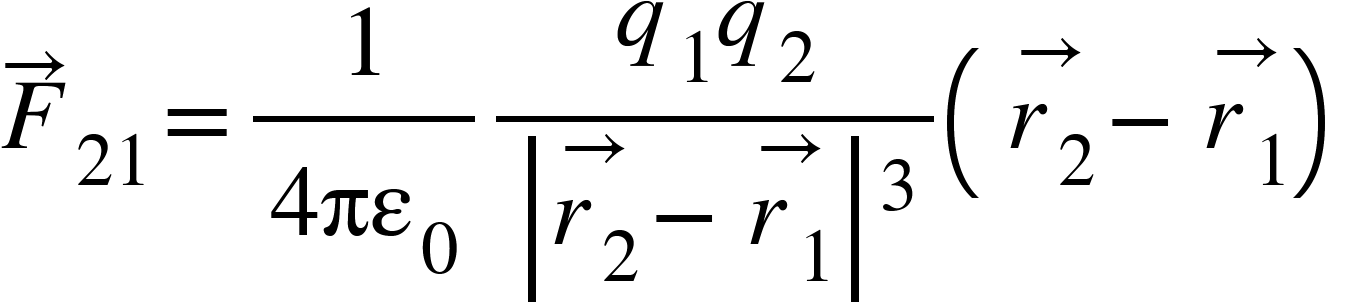
Superposition:
The principle of superposition gives the method to find the force on a charge when the system consists of many charges. When multiple charges are interacting, the total force on a given charge is given by,
Considering all the charges as negative, the electrostatic forces between these charges are the force of repulsion as like charges repel each other.
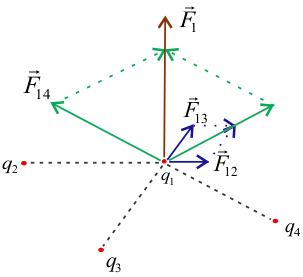
Figure:2.b
Therefore, using Coulomb’s law,
,
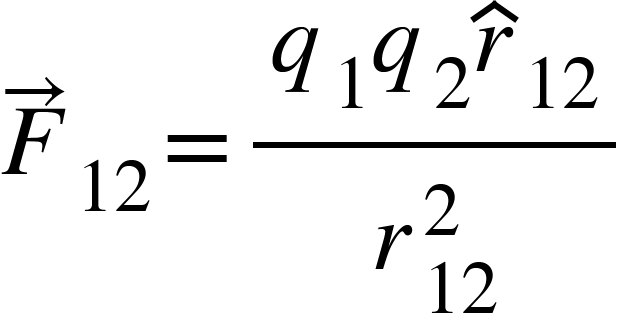Total force is given by,
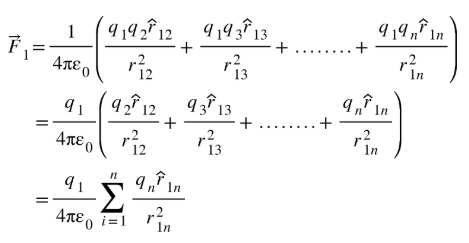
An example:
Three point charges $Q_{1}=4\times 10^{-9}C=4 nC$, $Q_{2}=6\times 10^{-9}C=6 nC$, and $Q_{3}=-3\times 10^{-9}C=-3 nC$form a right angle triangle. The distances between them are shown below. Find the magnitude of electrostatic force on charge $Q_{1}$due to $Q_{2}$ and $Q_{3}$. Given, dielectric constant = $9\times 10^{9}Nm^{2}C^{-2}$
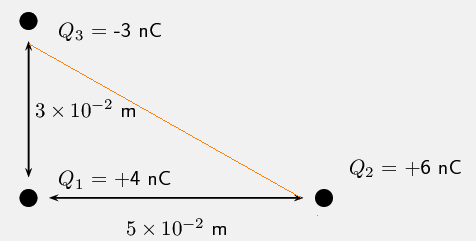
Figure:2.c
The magnitude of electrostatic force exerted by $Q_{2}$on $Q_{1}$ is given by,
$F_{2}=k\frac{4\times 10^{-9}\times 6\times 10^{-9}}{(5\times 10^{-2})^{2}}$
Or, $F_{2}=k\frac{4\times 10^{-9}\times 6\times 10^{-9}}{25\times 10^{-4}}$
Or, $F_{2}=k\frac{4\times 10^{-9}\times 6\times 10^{-9}}{25\times 10^{-4}}=0.96 k\times 10^{-14}$
Putting $k=9\times 10^{9}$, we have,
Or, $F_{2}=9\times 10^{9}\times 0.96 \times 10^{-14}=8.64\times 10^{-5}$N
The magnitude of electrostatic force exerted by $Q_{3}$ on $Q_{1}$ is given by,
$F_{3}=k\frac{4\times 10^{-9}\times (3\times 10^{-9})}{(3\times 10^{-2})^{2}}=9\times 10^{9} \times \frac{12\times 10^{-18}}{9\times 10^{-4}}= 12\times 10^{-5}$N
The magnitude of the resultant force is given by,
$F_{R}^{2}=F_{2}^{2}+F_{3}^{2}$
Or, $F_{R}^{2}=$$(8.64\times 10^{-5})^{2}+(12\times 10^{-5})^{2}$
Or, $F_{R}=\sqrt{(8.64\times 10^{-5})^{2}+(12\times 10^{-5})^{2}}$
Or, $F_{R}=\sqrt{(74.64\times 10^{-10})+(144\times 10^{-10})}$
Or, $F_{R}=\sqrt{(218.64\times 10^{-10})}$
Or, $F_{R}=1.479\times 10^{-4}$N.
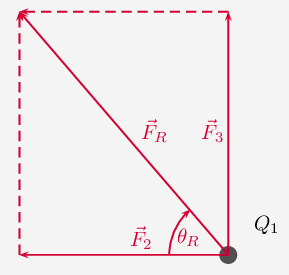
Figure:2.d
$tan \theta =$$12\times 10^{-5}$/$8.64\times 10^{-5}$
Or, $tan \theta =$$1.39$
Or, $\theta =tan^{-1}1.39=54.26^{0}$ to the negative x-axis.