Frictional force arises whenever two surfaces of two bodies come in contact with each other.
The frictional force is an example of a contact force. The magnitude of the contact forces on two bodies is equal opposite in direction.
Contact forces depend on the nature of the surfaces of the two bodies kept in contact.
Suppose, a block is kept on a horizontal surface.
Let $F_{c}$ is the contact force both the bodies exert on each other.
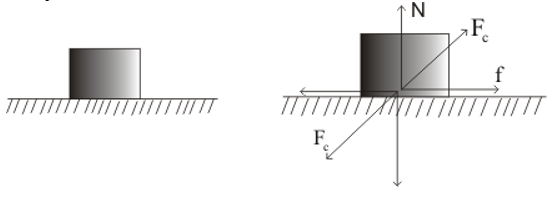
Figure: 18.a
Contact force F$_{c}$ can be resolved into two components. The component of F$_{c}$ along the normal to the surface is called normal contact force (N) and a component parallel to the surface is called friction (f).
Friction is of two types- static friction and kinetic friction.
Static friction:
Static friction comes into play when the bodies at rest.
For example, a heavy block resting on a surface cannot be moved easily until the magnitude of the applied force is increased. The force of static friction must be overcome by the applied force before the body at rest begins to move or slide.
The maximum value of static friction between the two surfaces in contact is known as limiting friction $f_{ms}$.
The magnitude of static friction $f_{s}$ cannot go beyond the magnitude of the limiting friction that is $f_{s} f_{ms}$.
This limiting friction is proportional to the normal contact force (N) between the bodies.
So, $f_{ms}\alpha N$
Or, $f_{ms}=\mu _{s} N$
Where $\mu _{s}$ is a constant known as the coefficient of static friction.
$\mu _{s}$ depends on the material and roughness of the surfaces of bodies in contact.
kinetic friction friction:
It arises between the moving surfaces or between the bodies in motion.
When the applied force becomes greater than limiting frictional force, then the body starts to move and kinetic friction comes into existence.
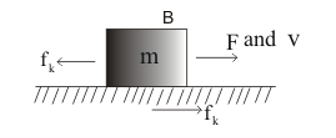
Figure: 18.b
Suppose a block $B$ of mass $m$ is at rest.
When the block is sliding over the surface each, the body exerts a frictional force on the other side parallel to the surface in contact
The force of kinetic friction $f_{k}$ and its magnitude is always less than the magnitude of limiting friction $f_{ms}$. Therefore, $f_{k}\le f_{ms}$
the kinetic friction force is proportional to the normal contact force.
So, $f_{k}\alpha N$
Or, $f_{ms}=\mu _{k} N$
Where $\mu _{k}$is a constant known as coefficient of kinetic friction. $\mu _{k}$depends on the nature of the two surfaces in contact.
Angle of friction:
The angle made by the resultant reaction force with the normal reaction force is known as the angle of friction.
Consider a block of mass $m$ resting on a horizontal surface.
The block’s weight $W=mg$ is balanced by the normal force $N$.
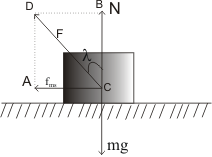
Figure: 18.c
Since $N$ and $f_{ms}$ are components of the contact force $F$ and $\lambda$ is the angle of friction, then
$F cos\lambda =N$ and $Fsin\lambda =f_{ms}$
Or,
$\tan \lambda =f_{ms}/N$
Also from the definition of static friction, we know that
So, $\tan \lambda =\mu _{s} N/N=\mu _{s} $
Therefore, the coefficient of static friction is equal to the tangent of the angle of friction.
Angle of Repose:
The angle which an inclined plane makes with the horizontal so that a body placed over it just begins to slide.
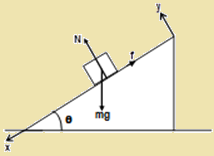
Figure: 18.d
Consider a body of mass resting on an inclined plane of inclination $\theta $. Obviously, If friction is large enough, the body will not slide down.
We have, $N=mg cos\theta $ and $f=mg sin\theta $
We have $f_{}\le \mu _{s}N$,
Or, $mg sin\theta \le \mu _{s}mg cos\theta $
So, $\tan \theta \le \mu _{s}.$
When $\theta $ is increased, then tan $\theta$ > $\mu$ . Thus sliding begins, and the angle $\theta _{r}=\tan ^{-1}\mu $. This angle is known as the angle of repose.