Gauss’s law is basically the relation between the charge distribution to the behavior of the electrostatic field in space.
Before we discuss Gauss’s law in detail, let us study the electric field due to continuous charge distributions.
Let us consider that charges on a surface are located very close together so that such a system of charges can be assumed to have a continuous distribution of charges.
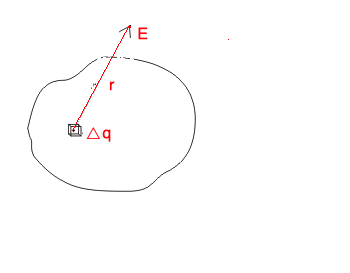
Figure:5.a
Let us divide the continuous charge distribution into small elements containing Δq amount of charge.
The electric field Eat a point, due to charge Δq at a distance ris given by,
![]()
r is the unit vector in the direction from charge towards that point.
Total electric field at that point due to all the charges is given by,
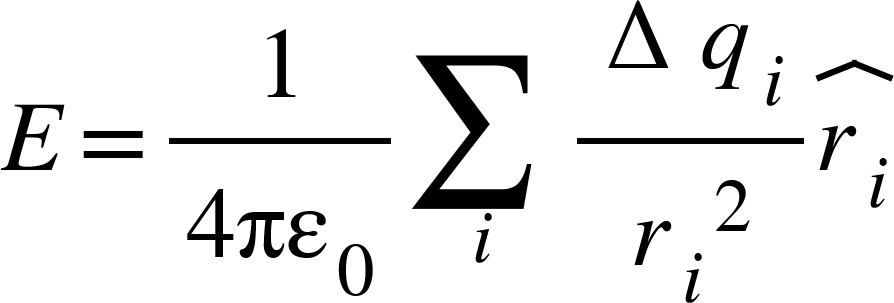
Since the charge is distributed continuously over some region, the sum becomes integral over the entire charge distribution.
Total field within the limit Δq→0 is,

Points to remember:
- If a charge q is uniformly distributed along a line of length L, the linear charge density λ is defined by λ=q/L. Its unit is C/m.
- If a charge distributed non-uniformly over a line, the linear charge density λ is given by, λ=dq/dL
- For a charge q distributed uniformly over a surface of area A, the surface charge density σ is σ=q/A. Its unit is C/m2.
- Similarly, the volume charge density ρfor uniform and non-uniform charge distribution is given by, ρ=q/Vand ρ=dq/dVrespectively. Its unit is C/m3.
Gauss’s law:
Gauss’s law in electrostatics states that the total electric flux through a closed surface is equal to the net electric charge enclosed by the surface divided by the free space permittivity.
Mathematically,
![]()
where E is the electric field flowing through small area element da and q is the net charge enclosed in it.
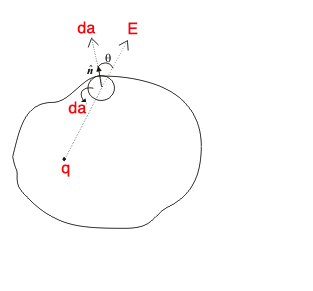
Figure:5.b
Proof of Gauss’s law:
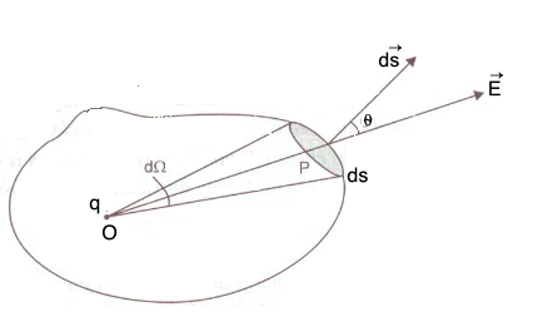
Figure:5.c
Consider a small area ds of the surface surrounding a point P. A charge qis placed at point O within the closed surface.
The electric flux through ds is given by,
![]()
The electric field strength at P (distance OP = r from O) is given by,
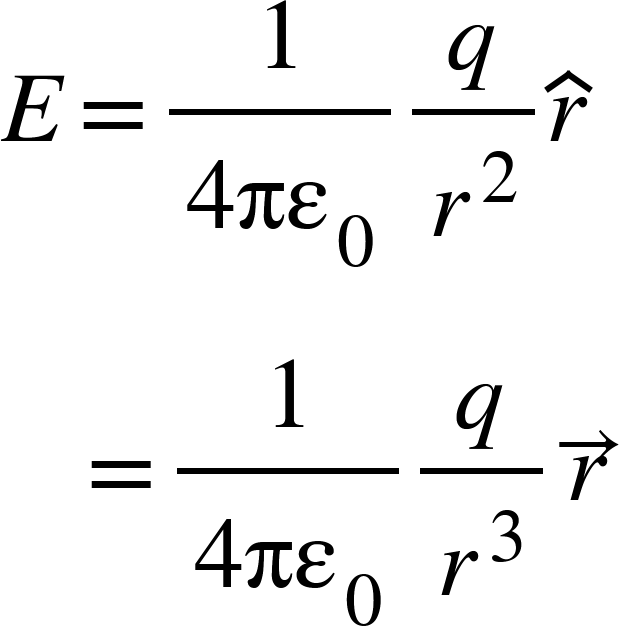
So, electric flux,
![]()
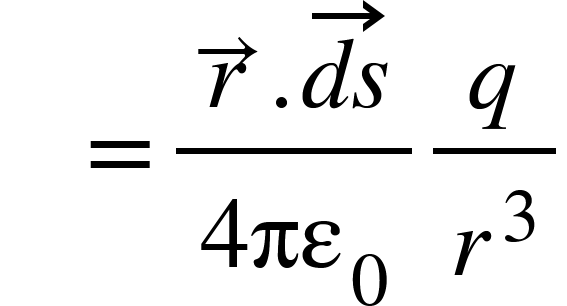
=q4πϵ0dΩ
Where dΩ is the solid angle subtended by area ds.
Electric flux through the entire closed surface,
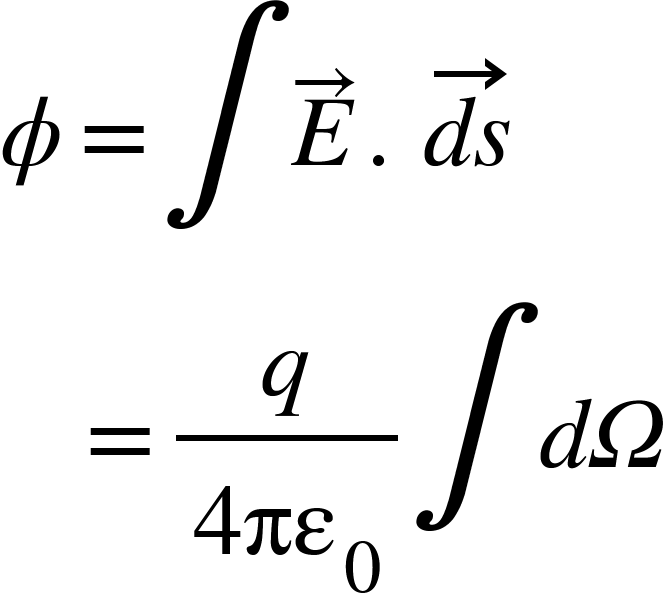
But dΩ is the solid angle to the entire closed surface at O, which is 4π
So,
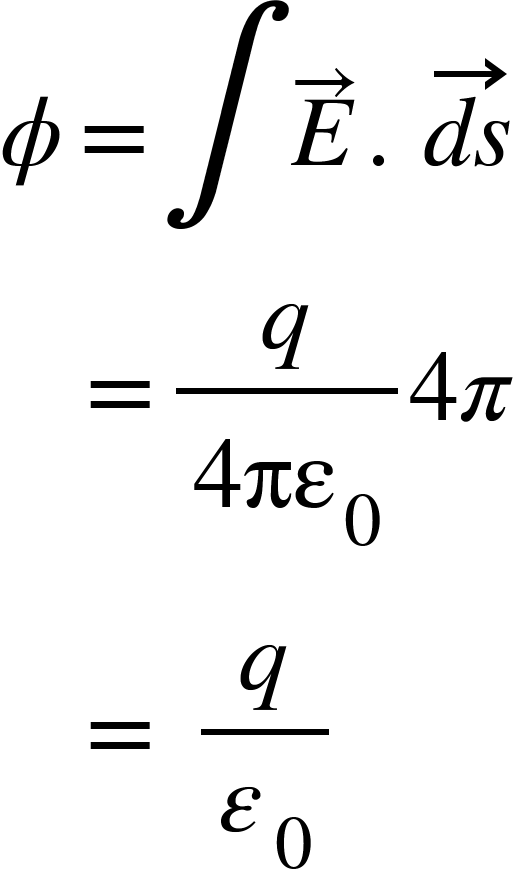
This is Gauss’s law.
Derivation of Coulomb’s law from Gauss’s law:
From Gauss’s law,
![]()
As E is constant at all points on the surface, then,
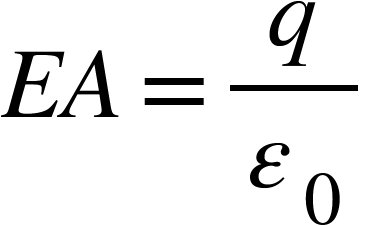
Where A=4πr2 = surface area of the sphere
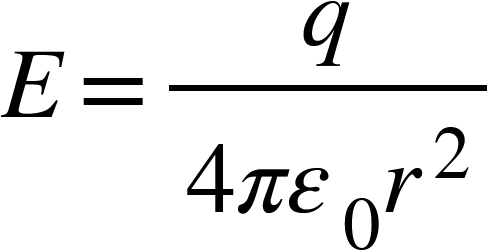
Now force acting on a point charge q1at a distance r from charge q is given by,
F=q1E
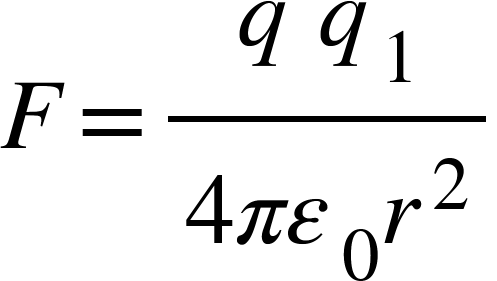
Which is Coulomb’s law.
Application of Gauss’s Law
In this module, you will learn about the Application of Gauss’s law.
Electric field due to line charge:
Consider a long thin uniformly charged wire. Electric field intensity have same magnitude at all points which are at the same distance from the line charge.
Let us imagine a Gaussian surface to be a right circular cylinder of radius r and length l with its ends perpendicular to the wire as shown below. Since the field is everywhere radial, electric flux through the two ends of the Gaussian surface is zero.
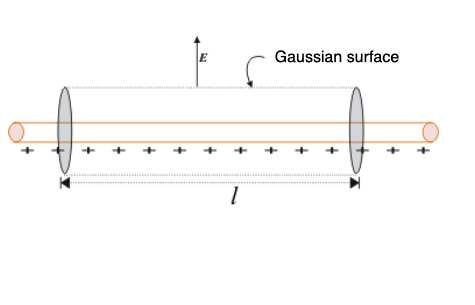
Figure:6.a
λ is the charge per unit length on the wire. Direction of electric field $EisperpendiculartothewireandcomponentsofE$ normal to end faces of cylinder makes no contribution to electric flux. Thus from Gauss’s law,
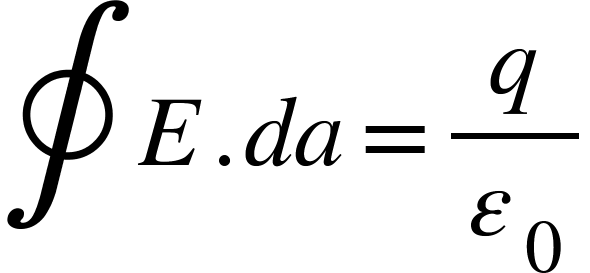
Since at all points on the curved surface E is constant, the surface area of the cylinder of radius r and length l is A=2πrl
Then,
![]()
Or, ∮E.da=E(2πrl)
Now total charge enclosed q=λl
Then,
Therefore, the electric field intensity of a long positively charged wire depends on the radial distance r of points from the wire.
Electric field due to charged solid sphere:
Imagine a Gaussian charged sphere of radius R and ris the radial distance where at any point we will calculate the electric field.
From Gauss’s law,
![]()
Where q is the charge enclosed.
Since the electric field points radially outwards we have,
![]()
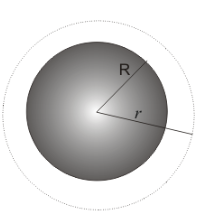
Figure:6.b
The magnitude of E is constant over the surface of Gaussian sphere. Therefore,
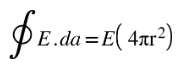
Where 4πr2 is the surface area of the sphere.
Then,
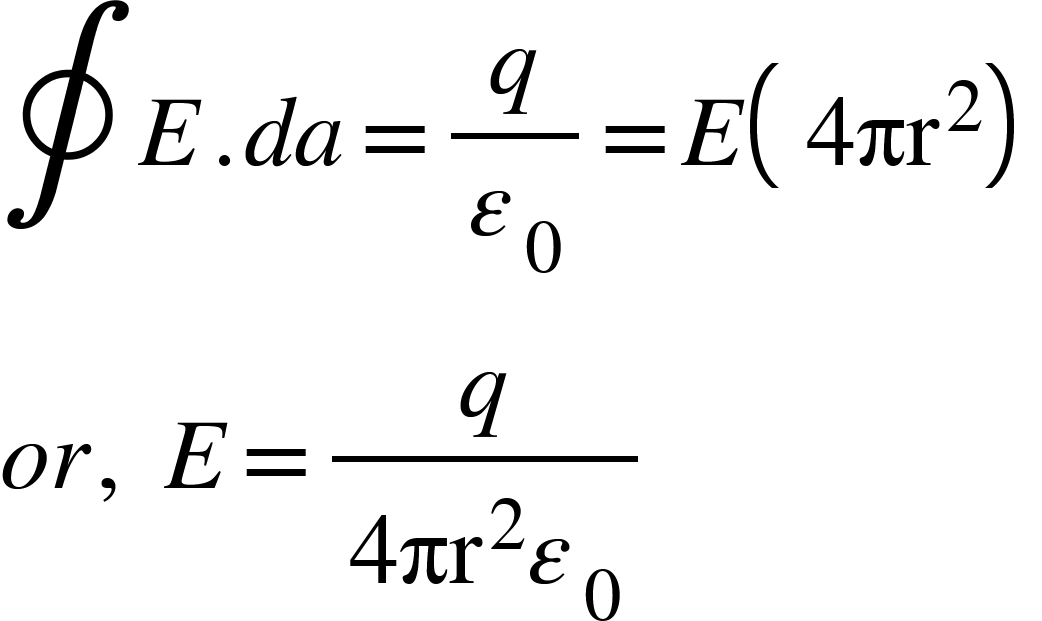
The electric field is directed outward if and inward if q>0 and inward if q<0. This is exactly the field produced by a charge q placed at the centre of the sphere.
Therefore, for points outside the shell, the electric field is exactly the same as it would have been as if the entire charge of the shell is concentrated at its centre.
Points to remember:
There is no charge inside the spherical shell. The surface charge density is dispersed outside the surface only, and hence,
![]()
Therefore, there is no electric field inside the spherical shell because of the absence of the enclosed charge.