Graphs of inverse trigonometric functions

The graph of y = sin x can be visuallised in the figure below:

Domain: all reals Range: [-1,1] Period: 2π Y-intercept: (0,0)

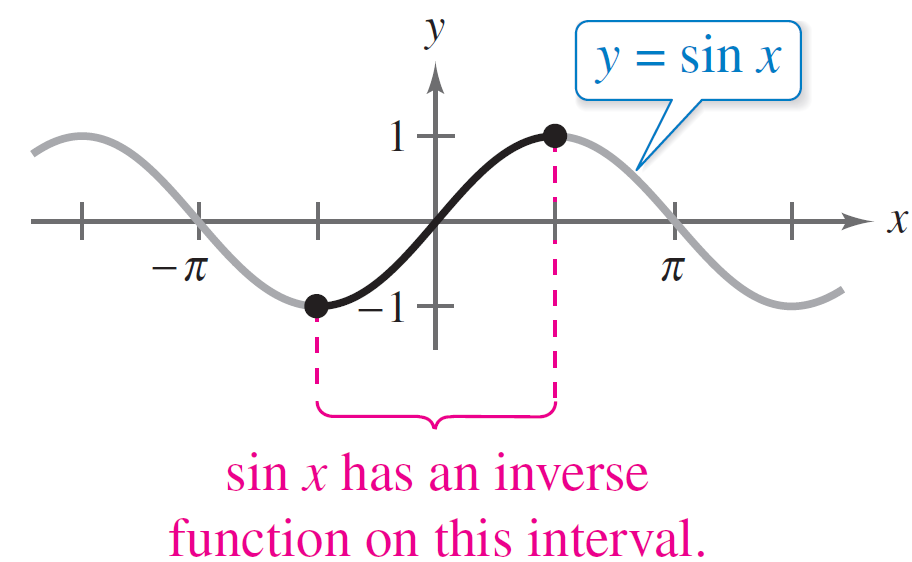
When you restrict the domain of sin x to the interval –π/2 ≤ x ≤ π/2, the following properties should hold:

1.y = sin x is an increasing function.

2.y = sin x utilizes full range of values, –1 ≤ sin x  ≤ 1.

3.y = sin x is a one-to-one function.

In conclusion, on the restricted domain –π/2 ≤ x ≤ π/2, y = sinx obtains a unique inverse function called the inverse sine function: y = arcs in x or y = sin^–1x. The inverse function is equivalent to the analogy of an inverse function notation f ^–1(x) which is not the same as (f)^-1.

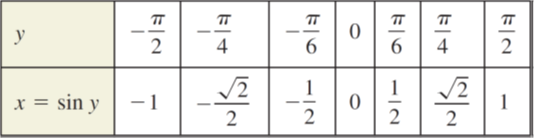
Using the domain: [-π/2 ;π/2] let’s plot the graph y = arcs in x. Remember that y = arcs in x can be written as sin y = x

The graph of y = arcsin x

Domain: $[$-1, 1$]$ Range: $[-\frac{\pi }{2},\frac{\pi }{2}]$

Similarly, we can use 1-1 cos x values to plot the graph of arccos x. The cosine function is a decreasing function and it forms one-to-one values on the interval 0  ≤ x ≤ π, as shown in the figure below:

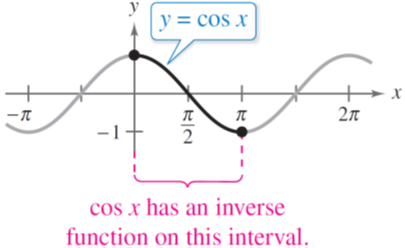
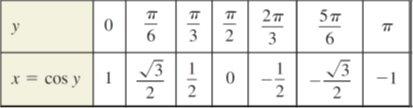
On this interval, the cos x has an inverse function denoted by y= arccosx or y = cos^–1x. Because y = arccosx and x = cos y mean the same for 0  ≤ y ≤ π, their graphs are the same, and can be confirmed by the following table of values.

The graph of y = arccos x

Domain: [-1, 1] Range: [0, π] Period: Y-int: [0, 0]

The other trigonometric functions require similar restrictions on therefor generating an inverse function.The domain of the section of the tangent that generates the arctan is $\frac{–\pi }{2},\frac{\pi }{2}$ and the inverse tangent function is denoted by y = arctan x or y = tan ^–1x. Since y = arctan x and x = tan y are the same for –2 <y<2 their graphs are the same, and can be confirmed by the following table of values.

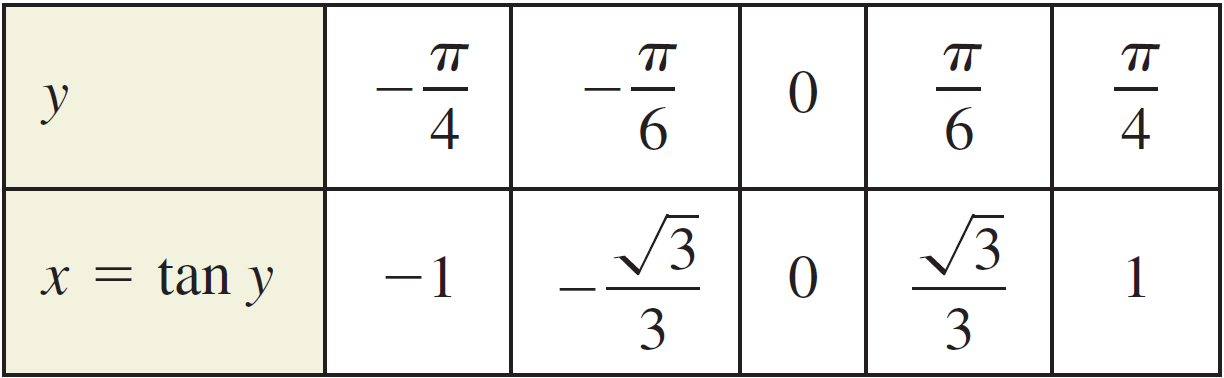
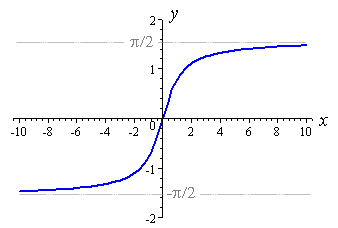
Domain: $[-\infty , \infty $$]$ Range: $[$$\frac{-\pi }{2}, \frac{\pi }{2}$$]$