1. The displacement of an object is given by the following equation. $x=2t+t^{2}_{}-3t^{3}$
Calculate the velocity of the object when its acceleration is zero.
We have, $x=2t+t^{2}_{}-3t^{3}$
Or, velocity $v=\frac{dx}{dt}=\frac{d}{dt}(2t+t^{2}_{}-3t^{3})$
Or, $v=2+2t-9t^{2}$\ldots \ldots \ldots \ldots \ldots (1)
Acceleration, $a=$$\frac{dv}{dt}=\frac{d}{dt}(2+2t-9t^{2})$
Or, $a=2-18t$
Or, $2-18t=0$, as acceleration is zero
Or, $t=2/18=1/9$
Putting this value in equation (1), we get,
$v=2+2\times \frac{1}{9}-9(1/9)^{2}$
Or, $v=2+\frac{2}{9}-\frac{1}{9}$
Or, $v=19/9$.
2. An object is released from a certain height under the influence of gravity. State the nature of the velocity-displacement graph.
For an object undergoing free fall, the equation of motion is given by,
$x=ut+1/2 gt^{2}=1/2 gt^{2}$, initial velocity u = 0
velocity $v=\frac{dx}{dt}=\frac{d}{dt}(1/2 gt^{2})$
Or, $v=gt$
Or, $t=v/g$
Putting the value of t in the above equation, we get,
$x=1/2 g \frac{v^{2}}{g^{2}}$
Or, $v^{2}=2gx$
This is an equation of parabola. Therefore, the velocity-displacement graph gives a parabolic path.
3. An object is released from a height H. During the journey, it covers $H/2$distance in time $t_{1}$ and the remaining distance in time $t_{2}$. Prove that $t_{1}$$>$ $t_{2}$.
For the first half, we have the equations of motion,
$H/2=1/2 gt_{1}^{2}$ ……………. (1)
$v=gt_{1}^{}$ ……………… (2)
For the second half,
$H/2=vt_{2}+1/2 gt_{2}^{2}$
Or, $H/2=gt_{1}t_{2}+1/2 gt_{2}^{2}$ …………….. (3)
Comparing equations (1) and (3), we get,
$1/2 gt_{1}^{2}=gt_{1}t_{2}+1/2 gt_{2}^{2}$
Or, $t_{1}^{2}=2 t_{1}t_{2}+t_{2}^{2}$
Or, $2 t_{1}t_{2}+t_{2}^{2}-t_{1}^{2}=0$
Applying the formula of quadratic equation, we get,
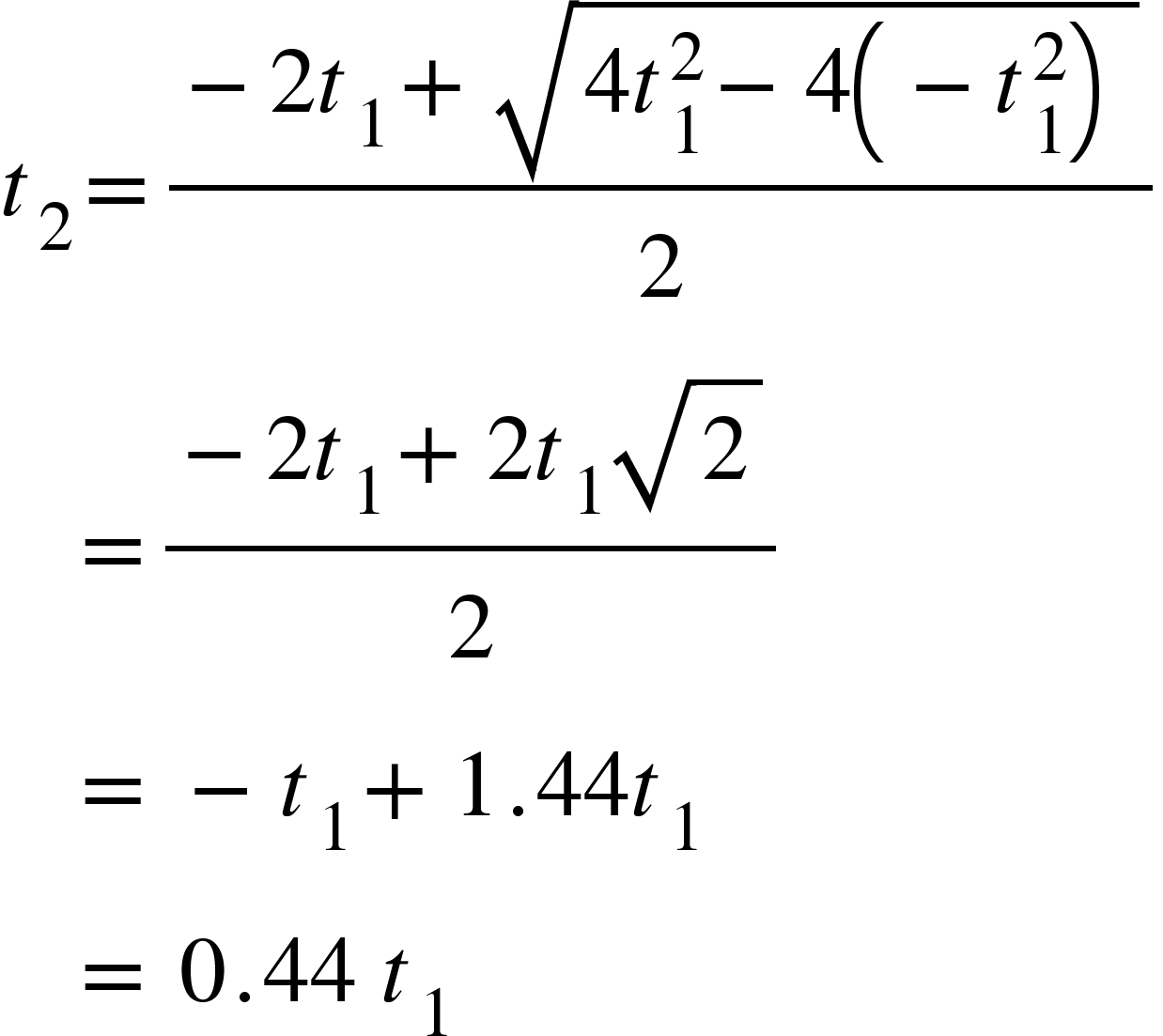
Therefore, $t_{1}>t_{2}$.
4. A stone of mass 0.01kg is released from the terrace of a building of height 70 m. Simultaneously another stone of mass 0.008kg is thrown up from the same place with a speed of 30 m/s. Calculate their relative speed.
For stone of mass 0.01kg, we apply kinematic equation,
$v_{1}=0-gt=-gt$
For a stone of mass 0.008kg, we apply the kinematic equation
$v_{2}=30-gt$
Relative velocity of first stone with respect to second stone,
$v_{12}=-gt-(30-gt)=-30$m/s
Similarly, $v_{21}=30-gt-(-gt)=30$m/s
So, the relative velocity is 30 m/s.
5. A racing car moves along a circular path of radius R at speed v so that it makes one revolution in every T seconds. If the car moves around a different circular path of radius 4R so that it takes one revolution in every T/2 seconds, then find the ratio of the magnitude of centripetal acceleration.
We have centripetal acceleration, $a=V^{2}/R$
Now, $V=2\pi R/T$
So, for the first track, centripetal acceleration $a_{1}^{}=\frac{4\pi ^{2}R^{2}}{RT^{2}}=\frac{4\pi ^{2}R^{}}{T^{2}}$
For the second track, $V=2\pi 4R/(T/2)=16\pi R/T$
For the second track, centripetal acceleration $a_{2}^{}=\frac{16\times 16\pi ^{2}R^{2}}{4RT^{2}}$
Or, $a_{2}^{}=\frac{64\pi ^{2}R^{}}{T^{2}}=16 a_{1}$
Or, $a_{1}$/$a_{2}^{}$=1/16
Or, $a_{1}:a_{2}=1:16$.
6. A bus starts from rest and accelerates uniformly over a time of 6 seconds for a distance of 110 m. Calculate the acceleration of the car.
We have, initial velocity, $u=0$, $t=6s$, $s=110m$, $a=?$
Using kinematic equation,
$s=ut+1/2 at^{2}$
Or, $110=0+1/2 (a\times 36)$
Or, $36a=220$
Or, $a=6.11 m/s^{2}$.
7. Four cyclists A, B, C and D are in motion. Their relative velocities are given below:
= 20 m/s towards north
= 20 m/s towards east
= 20 m/s towards south
Calculate 
.
We have,
……….(1)
…………..(2)
………….(3)
Subtracting equation (2) from equation (1), we get,
……………..(4)
Adding equation (3) and (4), we get
Or, 
= $-20{i}$
So, 
= 20 m/s towards west.
8. The displacement (in meter) of an object moving along x-axis is given by $x=9t+4 t^{2}$. Calculate Instantaneous velocity at $t=2s$.
$v=dx/dt=\frac{d}{dt}($$9t+4 t^{2}$)
Or, $v=9+8t$
Instantaneous velocity at $t=2s$is $v=9+8\times 2=25$m/s.
