At the very beginning, getting to know about linear inequalities is something important.
What are linear inequalities?
As the name suggests, an inequality could be described as the relationship between two different quantities that aren’t equal. An inequality is known to be an open sentence which includes signs like$<,>,\le ,\ge $. Inequalities could be posed like questions much similar to equations and are solved in the same step-by-step order.
Solving Linear Inequalities
The graph for a linear inequality with one variable is likely to be a number line. In order to show < and >, open circles are to be used and to show ≤ and ≥.
Now, consider the graphs for the condition $x>-3$.
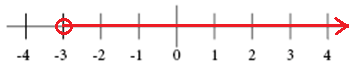
And also, the graph for the condition $x\ge 2$.

Inequalities that are known to possess similar solutions are addressed as equivalent. There are varying properties for both equalities and inequalities. All of these properties would be true for also the inequalities that involve ≥ and ≤.
The first one is the addition property; this property states that adding up the same number on both sides of the inequality will subsequently produce an equivalent inequality. This means:
If $x>y$ then $x+z>y+z$
If $x<y$ then $x+z<y+z$
Next is the subtraction property which states that the same number is subtracted from both sides of inequality will result in an equivalent inequality. This implies:
If $x>y$ then $x-z>y-z$
If $x<y$ then $x-z<y-z$
The following is the multiplication property of inequality which states that multiplying both sides of an inequality with certain positive numbers will result in producing an equivalent inequality. This implies:
If $x>y$ and $>0$ , then $xz>yz$
If $x<y$ and $z>0$, then $xz<yz$
Also, multiplication with a negative number on every side of inequality would not produce an equivalent inequality unless the direction of the inequality symbol is also reserved.
If $x>y$ and $z>0$, then $xz<yz$
If $x<y$ and $ z>0$, then $xz>yz$
Similar would be the case with division property of inequality
The division of both sides of inequality is likely to produce an equivalent inequality. This means:
If $x>y$ and $z>0$, then $\frac{x}{z}>\frac{y}{z}$
If $x<y$ and $z>0$, then $\frac{x}{z}<\frac{y}{z}$
In order to solve any multi-step inequality, you will have to do just what you did while solving multi-step equations. It would be preferable to pursue one thing at a time and begin with isolating the variables from the constants. While solving multi-step inequalities, it is necessary not to miss out on reversing the inequality sign while division or multiplication with negative numbers.