The mean of a discrete random variable X can be explained as a weighted average of the possible values that the random variable contains. Contrary to the sample mean, which gives each observation equal weight, random variable mean weights each outcome xi as per its probability, pi. The commonly used symbol for the mean or expected value of X) is μ, and it is formally defined by
μ = E(x)= ∑xip(xi)
where xi= the value of the random variable and P(xi) = the probability corresponding to a particular x value.
Example: Find the mean for the following probability distribution shown in the table below:
| Value of X | 0 1 2 3 |
| Probability | 0.064 0.288 0.432 0.216 |
The mean µ of X is
µ = (0*0.064) + (1*0.288) + (2*0.432) + (3*0.216)
= 1.8
The variance of a discrete random variable X measures the spread, or variability, of the distribution, and is defined by A weighted average of squared deviation about the mean
σ2 = E[(xi – μ)2] = ∑ (xi – μ)2p(xi)
Standard deviation: S.D =
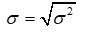
Example: Find the variance for the table above:
The variance σ2 of X is
σ2 = 0.064*(0−1.8)2 + 0.288*(1−1.8)2 + 0.432*(2−1.8)2 + 0.216*(3−1.8)2
= 0.20736 + 0.18432 + 0.01728 + 0.31104
= 0.72
the square root of Var X provides the SD: SD = 0.85
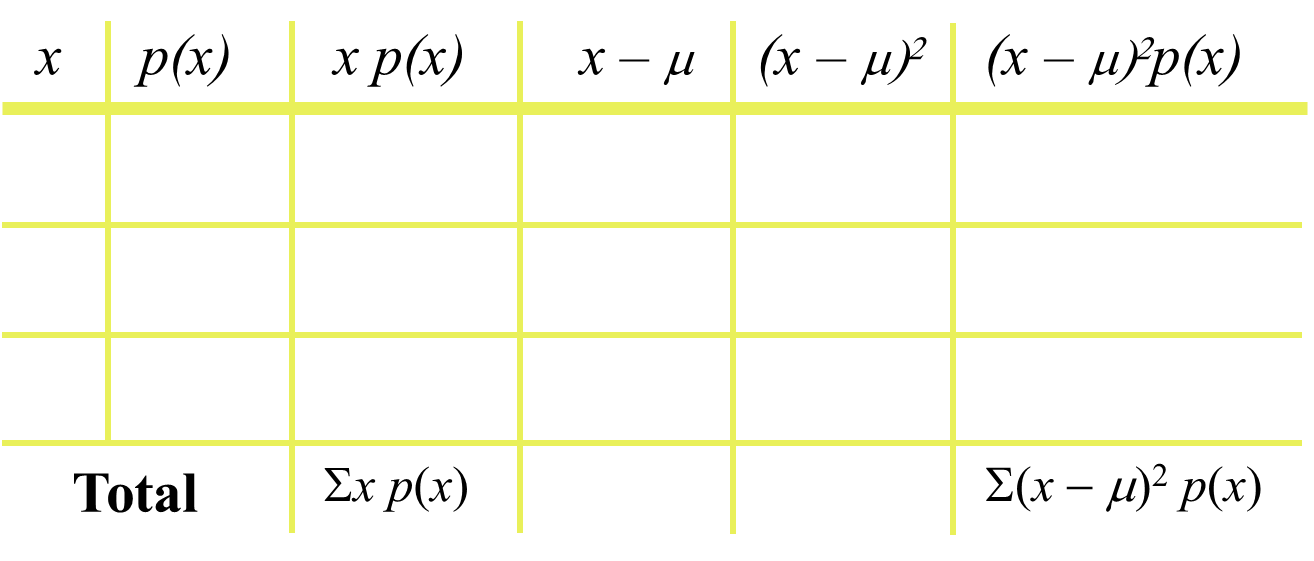
You can use the following table for calculating the variables:
Variance and mean are related to another relationship:
σ2=E(Xi – μ)2 = E(Xi2 – 2Xiμ + μ2)
= E(Xi2 – 2[E(Xi)]2 + [E(μ)]2
= E(Xi2) – [E(μ)]2
E(Xi2) =
Example:
Two cards are drawn one after another without replacement from a well-shuffled pack of 52 cards. Find the mean, variance and standard deviation of the number of queens.
Solution: Let Q be the number of queens in a draw of two cards. Therefore, Q is the random variable that assumes either 0, 1 or 2 values.
P(Q=0) = $^{48}$C$_{2}$/$^{52}$C$_{2}$ = $\frac{\frac{48!}{2!(48-2)!}}{\frac{52!}{2!(52-2)!}}=\frac{48\times 47}{52\times 51}=\frac{188}{221}$
P(Q = 1) = $^{4}$C$_{1}$? $^{48}$C$_{1}$ / $^{52}$C$_{2}$$\frac{4\times 48\times 2}{52\times 51}=\frac{32}{221}$
And P(Q = 2) = $^{4}$C$_{2}$/$^{52}$C$_{2}$ = $\frac{4\times 3}{52\times 51}=\frac{1}{221}$
Hence we can summarize the results in a probability distribution table for Q such that
| Q | 0 | 1 | 2 |
| P(Q) | 188/221 | 32/221 | 1/221 |
Mean of Q = E(Q) = $0\times \frac{188}{221}+1\times \frac{32}{221}+2\times \frac{1}{221}=\frac{34}{221}$
E(Q2) = =
Var(Q) = E(Q2) – [E(Q)]2= $0^{2}\times \frac{188}{221}+1^{2}\times \frac{32}{221}+2^{2}\times \frac{1}{221}=\frac{36}{221}$
S.D = $\sqrt{\frac{6800}{221^{2}}}=0.37$