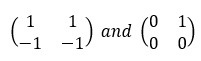Noncommutativity of multiplication of matrices and existence of non-zero matrices whose product is the zero matrices (restrict to square matrices of order 2)
Matrix multiplication is not commutative: AB ≠ BA.
Example: Consider the following example, calculate AB and BA

Because A has a dimension of 2 x 2 and B has a dimension of 2 x 3, the product AB is defined and it has dimension 2 x 3.
We can thus write:

Therefore, we define C =AB = [cij], here the entry of c11 is the inner product of the first row of A and the first column of B as shown below:
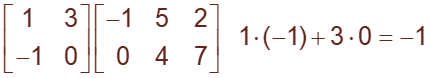
Similarly, we can calculate the remaining elements of the product as follows:
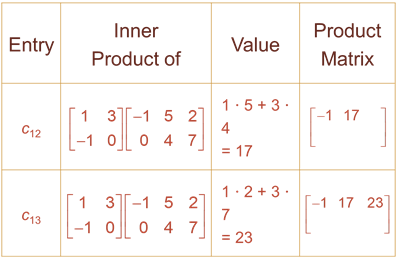
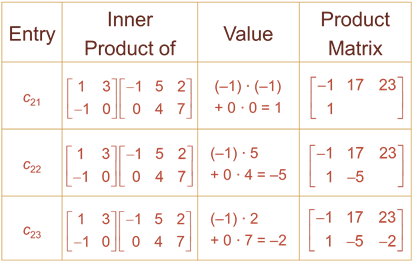
Thus, we obtain:
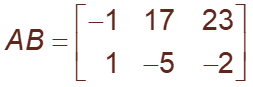
However, in this case the product BA is not defined. The dimensions of B and A are 2 x 3 and 2 x 2 respectively.The inner two numbers are not the same.So, the rows and columns won’t match up when we try to calculate the product.
Example: Consider the following example, calculate AB and BA

In this case, because both matrices A and B have dimension 2 x 2, both products AB and BA are defined, and each product is also a 2 x 2 matrix.
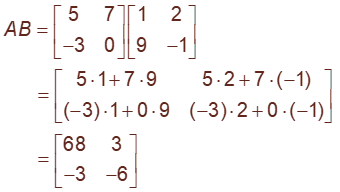
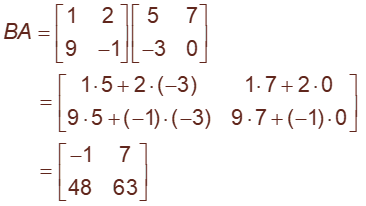
This shows that, in general, AB ≠ BA. In fact, here AB and BA don’t have even a single entry in common.
Zero matrix: product of two non zero matrices
For real number a and b, if ab = 0 then either a – 0 or b = o. But this property is not true for matrices
Example: Find AB when
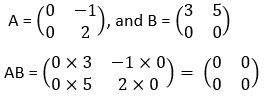
The above example shows two non zero matrices with a zero matrix product. Hence it is not necessary that of the matrices be a zero matrix to satisfy this property.
Example: Find two matrices A of 2X2 order such that A$^{2}$ = 0 but A ≠ 0
Solution: Let A be a 2X2 matrix such that
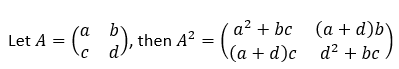
Now find a, b, c, d such that they satisfy the equality:
![]()
This means that, a + d = 0 and ad – bc = 0 (determinant=0). Hence a = -d = 1, b = -c = 1 or a = d = 0, b = 0, c = 1.
Then the matrices are not 0 but their squares are 0