Pascal’s triangle refers to a triangular pattern, series or the array of binomial coefficients. This triangle is named after a famous French philosopher and mathematician, Blaise Pascal. Pascal’s triangle’s beauty lies in its simplicity.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
How to Make Pascal’s Triangle
- On paper’s top, write “1” number in the centre
- Now, in the next row, write two of 1’s numbers, which forms a triangle.
- On each successive row, begin and end with 1’s in each of the rows and calculate the internal term by adding the 2 numbers which are present in the above row.
The explanation through the diagram is given below:
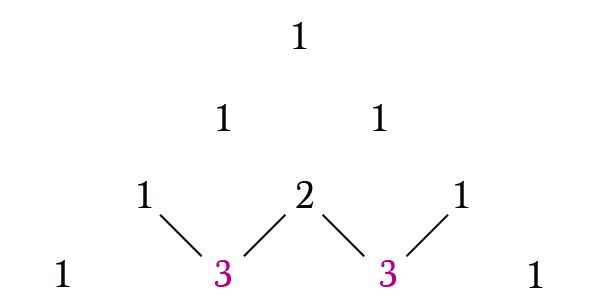
The Pascal’s triangle consists of:
Hidden numbers:
- The first two columns are known as the natural numbers.
- Next column is named as the triangular numbers.
- Likewise, the 4th column is defined as the tetrahedral numbers
- Hence, the columns in this way describe the “simplicies” which are defined as triangle’s extrapolations or also termed as the tetrahedron idea in the field of arbitrary dimensions.
- And the series goes on like, the next column is called the 5-simplex numbers, which will be followed by 6-simplex numbers, then 7-simplex numbers, and so on.
This special triangle has got Powers of Two
If you take the sum of each of the rows, then you’ll be getting the power belonging to base 2, which will be starting with 2⁰=1.
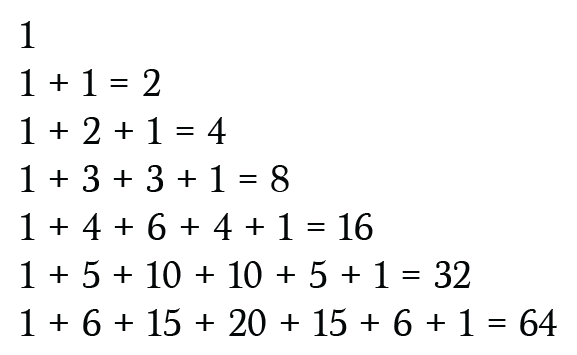
Adding the rows discloses the powers, having base 2
Powers of Eleven
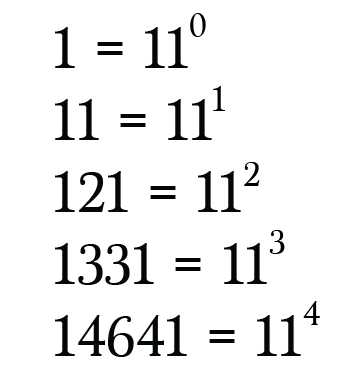
The Pascal’s triangle even uncovers the powers having base 11. Also, the difficulty comes when there are single digits, but what to do when there are double-digit numbers?
So, what you have to do is carry tens place on to the number present on its left side.
![]()
From the above explanation, showing to take carry place of tens in the sixth row to get 11⁵
Pascal’s triangle reflects Perfect Squares:
We can place natural numbers’ perfect squares in column 2 by adding the no. the right side with the given below number to the right side.
Let’s say:
- 3² → 3+6 = 9
- 4² → 6+10=16
- 5² → 5 + 20 = 25
and the series continues like this …
The Fibonacci Sequence
To reveal the Fibonacci Sequence, the sum of the diagonals present on the left side of Pascal’s triangle.
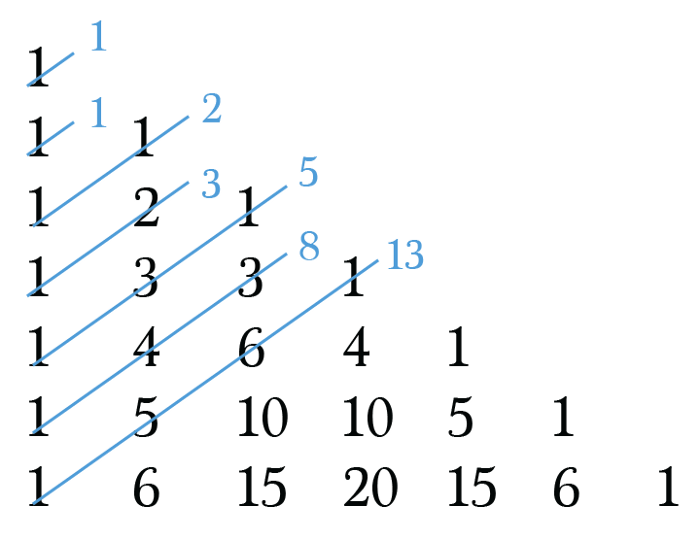
First seven nos. Present in the Sequence of Fibonacci as shown in the above diagram – 1, 1, 2, 3, 5, 8, 13, … is seen in Pascal’s Triangle
The Sierpinski Triangle
Using the initial orientation regarding Pascal’s triangle, shade or color all odd numbers and as a result, you will find a picture which looks exactly similar to the popular fractal Sierpinski Triangle.
Pascal’s Triangle act as Combinatorics
Probably, one of the most unusual relationships which are noticed in Pascal’s Triangle is – How you can use the method of determining the combinational or combinatorial numbers.
Recalling the formula for combinatorics. Here, you see that in each of the rows of Pascal’s triangle, the row no. is ‘n’ having a kth entry in that particular row, when you count from the value 0.
In this case, Pascal’s triangle can also be referred to as “n choose k” triangle.
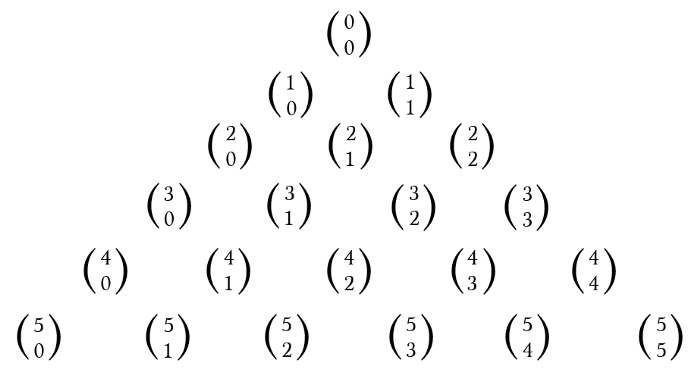
Pascal’s Triangle’s first six rows are represented with the help of Combinatorial Notation
So, if there’s a need for the calculation of 4, then you’ve to choose 2 and see the fifth row, 3rd entry and as we are counting from zero, you’ll be getting the solution as 6.
Expansion of Binomials
Assume that there’s the binomial (x + y) and you’ll be thinking to raise it to 2nd or 3rd power for example. Generally, you’ll be needing to pass through a hectic multiplying process, but with the use of Pascal’s Triangle, you can simply avoid the difficulty and can easily get the answer!
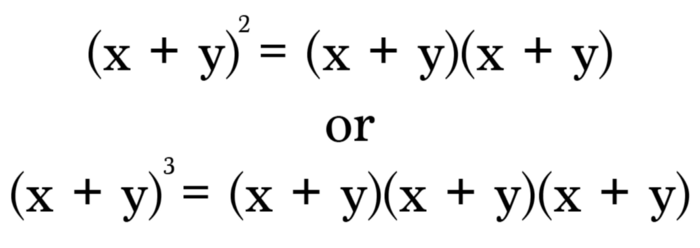
The Standard method of multiplying binomials
For instance, if you expand (x+y)³. Because we are in the process 0f raising the factor (x+y) to its 3rd power, therefore, we make use of the values in the 4th row of Pascal’s Triangle in the form of coefficients of your given expansion. Accordingly, fill x & y terms as mentioned below.
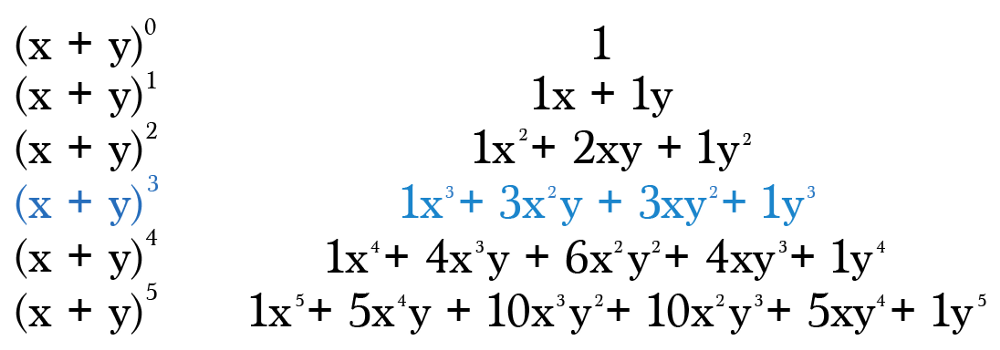
Conclusion:
So, Pascal’s triangle has significant usage in Indian Mathematics!