Straight Lines: Equation of a line – point-slope form
The slope-intercept form is simple to remember and use but it has one major disadvantage. We must know the y-intercept in order to use it. Generally, we do not know the y-intercept, we only know one or more points (that are not the y-intercept). In these cases, we can’t use the slope-intercept equation, so we will use a different more flexible formula. If we let the slope of an equation be m, and a specific point on the line be (x1, y1), and any other point on the line be (x, y) then we can derive another formula.
For a non-vertical line that passes through the point (x1, y1) with a slope of m.
Recall the slope formula
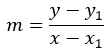
Now, multiply both sides by (x − x1)

A linear equation that written in the format shown above is in point-slope form. The graph of this equation is a line with slope m that passes through the point (x1, y1).
Note that there is a difference between the meaning of (x1, y1) and (x, y). Here, (x1, y1) is a specific point on the line while (x, y) represents ANY point on a line.
We need to be very careful with the transfer of negative sign in the point-slope formula. To obtain the equation of a line, we will always need to know the slope. If we don’t know the slope, we will have to manipulate the equation to find it first before we can get an equation.
Example 1. Given two points, (2, -3) and (4, -2) write the equation of a line in point-slope form
Step 1. Find the slope.
![]()
Step 2. Place a point and the slope into point-slope form.
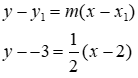
Step 3. Write in the correct order of point-slope form.
![]()
Often, we prefer answers to be written in slope-intercept form. If the directions ask for the answer in the slope-intercept form we will simply distribute the 1 slope, then solve for y. Simplify using the distributive property, then move the constant to the right side & combine like terms
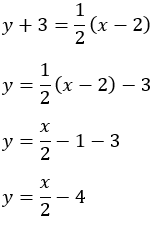
Example 2. Write the Equation in Point-Slope Form = -1/3 and coordinates (-1, -6)
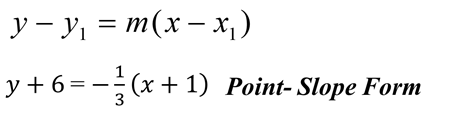
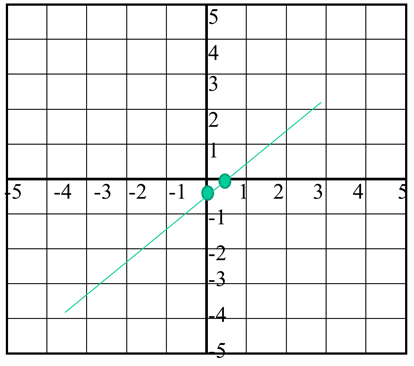
Example 3. Plot a graph of $y-1=\frac{2}{3}(x-2)$
Step 1. Find y when x = 0
$y-1=\frac{2}{3}(0-2)$
$y-1=\frac{-4}{3}$
$3(y-1)=-4$
$3y=-4+3$
$y=-1/3$
Step 2. Find x when y = 0
$0-1=\frac{2}{3}(x-2)$
$\frac{-3}{2}=x-2$
$\frac{-3}{2}+2=x$
$\frac{1}{2}=x$
Step 3. Using two points in a line, plot the graph.
` 
Example 4. Convert the standard form of the equation to point-slope form.
-4x +y = -11
Step 1. Convert the equation to point- intercept form to find the slope.
$y=4x-11$
m=4
Step 2. Assume x$_{1}$ = 1, find y$_{1}$
$y=4-11$
$y=-7$
Step 3. Substitute the values in the equation
$y+7=4(x-1)$