See the word problems solved here to get the basic ideas on how you should be using properties of set’s union and intersection.
Word Problems:
Example 1. Let finite sets, Set A and Set B like n (A) = 25, n (B) = 29; n (A ∪ B) = 38, so, find –
n (A ∩ B).
Solution:
Using formula of union
= n (A ∪ B) = n (A) + n (B) – n (A ∩ B)
then, n (A ∩ B) = n (A) + n (B) – n (A ∪ B)
= 25 + 29 – 38
= 54 – 38
= 16
Example 2. If n (A – B) = 20, n(A ∪ B) = 60 and n(A ∩ B) = 30, then find n(B).
Solution:
Using formula,
n (A∪B) = n (A – B) + n (A ∩ B) + n (B – A)
60 = 20 + 30 + n(B – A)
60 = 50 + n(B – A)
n(B – A) = 60 – 50
n(B – A) = 10
Now, n(B) = n(A ∩ B) + n(B – A)
= 30 + 10
= 40
Different categories of word problems regarding sets:
Question 3. A group of 70 people is there, 50 people like hot soups, and 28 people like cold soups, and each individual like at least one out of 2 soups. How many people like tea and coffee?
Solution:
Let take,
A = Set of individuals liking cold soups.
B = Set of individuals liking hot soups.
Given,
- (A ∪ B) = 70n
- (A) = 50
- n(B) = 28 then;
As per formula , n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 50 + 28 – 70
= 78 – 70 = 8
= 8
Thus, 8 people like coffee and tea
Another Example:
In a school where 600 students are there, 200 like history subject, 160 like English and 50 like both History and English. Find the number of students who like
- Students who like History; not English
- Students who like English; not History
- Students who either like History or English
Solution
Let the total number of students be U that is, the universal set.
Assuming A = set of a number of students who favor History.
Assuming B = set of a number of students who favor English.
Here, n (U) = 600 n (A) = 200 n (B) = 160 n (A∩B) = 50
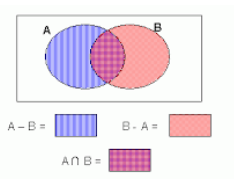
Here, you have to determine the number of students who favor History but not English, so to find A-B:
As shown in the Venn diagram,
A = (A-B) ∪ (A∩B)
n (A) = n (A-B) + n (A∩B)
n (A-B) = n (A) – n (A∩B)
= 200 – 50 = 150
Therefore, the numbers of students who favor only History but not English = 150
Here, you have to determine the number of students who favor English but not like History, so to find B-A:
B = (B-A) ∪ (A∩B)
n (B) = n (B-A) +n (A∩B)
n (B-A) = n (B)- n (A∩B)
= 160 – 50 = 110
Therefore, the numbers of students who favor only English but not History are= 110.
Here we have to find the number of students who like either English or History.
n (A∪B) = n (A) + n (B) – n (A∩B)
= 200 + 160 – 50
= 310
Next Word Problem:
Question: A competition was held in the school where students were given awards in different groups. 46 medals were given in dance, 22 medals in sports, and a total of 15 medals in English debate. If these medals were given to 44 total students and only 5 students got medals in each of the 3 groups, then how many medals are acknowledged in exactly 2 of these groups?
In a competition, a school awarded medals in different categories. 36 medals in dance, 12 medals in dramatics and 18 medals in music. If these medals went to a total of 45 persons and only 4 persons got medals in all the three categories, how many received medals in exactly two of these categories?
Solution:
Assuming A = set of students who got medals in dance.
B = set of students who got medals in sports.
C = set of persons who got medals in English Debate.
Given,
n(A) = 46 n(B) = 22 n(C) = 15
n(A ∪ B ∪ C) = 44 n(A ∩ B ∩ C) = 5
As we know the number of elements which belongs to exactly 2 out of three sets A, B, C
= n(A ∩ B) + n(B ∩ C) + n(A ∩ C) – 3n(A ∩ B ∩ C)
= n(A ∩ B) + n(B ∩ C) + n(A ∩ C) – 3 × 4 ……..(i)
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) + n(A ∩ B ∩ C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C)
Therefore, n(A ∩ B) + n(A ∩ C) + n(B ∩ C) = n(A) + n(B) + n(C) – n(A ∪ B ∪ C) + n(A ∩ B ∩ C)
From (i) the required number
= n(A) + n(B) + n(C) + n(A ∩ B ∩ C) – n(A ∪ B ∪ C) – 12
= 46 + 22 + 15 + 4 – 44 – 12
= 85 – 12
= 73