Properties of addition, multiplication and scalar multiplication in matrices

Commutative Law:

A + B = B + A

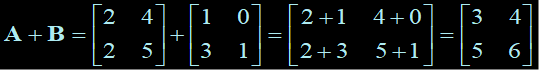
The definition of subtracting two real numbers a and b is a – b = a + (-1)b or a + the opposite of b.

We can define subtraction of matrices similarly, therefore,when A and B are two matrices of the same dimensions, then

A – B = A + (-1)B, where -1 is a scalar element

For subtraction:

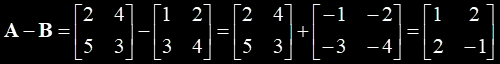
Associative Law:

1. A + (B + C) = (A + B) + C = A + B + C
2. A + (-A) = 0 (where –A is the matrix composed of –a_ij as elements)

The properties of matrix addition and scalar multiplication are similar to the properties of addition and multiplication of real numbers. The addition of real numbers is such that the number 0 follows with the properties of additive identity. This means, c + 0 = c for any real number. Similar properties hold for matrices:

Assuming that matrices A, B and C are conformable for the operations indicated and c,d etc. denote scalar quantity then the following are true:

1. AI = IA = A(scalar identity)
2. (cd)A = c(dA) (associative property of scalar multiplication)
3. A + O = A(additive identity)
4. c(A +B) = cA + cB(distributive property)
5. (c + d)A = cA + dA( distributive property)

For example:

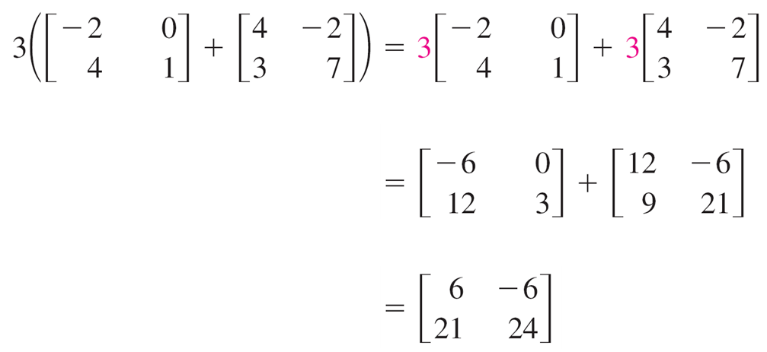
The general properties for matrix multiplication are as follows,

1. (AB)’ = B’A’(multiplication and transposition)
2. A(BC) = (AB)C = ABC – (associative law)
3. A(B+C) = AB + AC – (first distributive law)
4. (A+B)C = AC + BC – (second distributive law)
5. c(AB) = (cA)B = A(cB)( associative property of scalar multiplication)

The division of matrices is not possible. However, matrix inversion works in some sense as a procedure similar to division.

The inverse of a matrix [A], expressed as [A]^-1, is defined as:

NOTE: the inverse of a matrix [A] exists ONLY if where = the equivalent determinant of matrix [A]

Recall that,

1. AB may or may not be equal to BA, hence BA may not be conformable
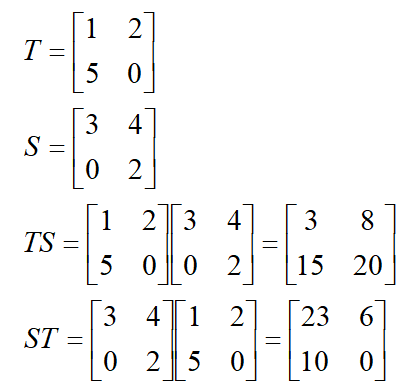
2. If AB = 0, neither A nor B necessarily be equal to 0
3. If AB = AC, B may or may not be equal to = C

Properties of transposed matrices:

1. (A+B)^T = A^T + B^T
2. (AB)^T = B^TA^T
3. (kA)^T = kA^T
4. (A^T)^T = A