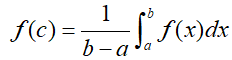Basic properties of definite integrals and evaluation of definite integrals
Properties of Basic Integrals
If y = f(x) is considered as a nonnegative and integrable function over a closed interval [a,b], then the area under the curve of y = f(x) from point a to b is the integral of f from point a to b, and we can conclude that:
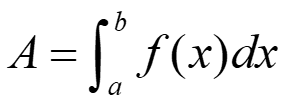
If the graph is nonpositive from a to b then
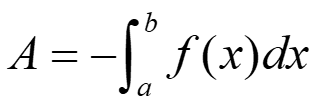
For an integrable function = (area above the x -axis) – 9 area below the x axis)
If f(x) = c, such that c is a constant on the interval [a,b], then can assume that:
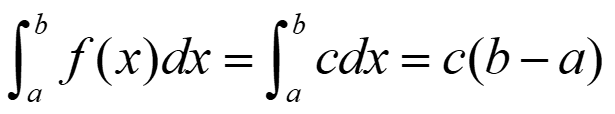
We can use integrals to calculate areas and vice verse.
Example:
Using areas, evaluate the integral: $\int_{-2}^{3}{x+1 dx}=[\frac{x^{2}}{2}]_{-2}^{3}+\lbrack x\rbrack
_{-2}^{3}=\lbrack \frac{9}{2}-\frac{4}{2}\rbrack +\lbrack 3-(-2)\rbrack
=\frac{5}{2}+5=\frac{15}{2}$
Rules of definite integrals:
Order of integration:
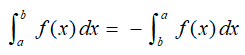
Integral at one point:
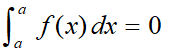
Integral from b to a:
$\int_{a}^{b}{f(x)dx=}\int_{a}^{b}{f(a+b-x)dx}$
Integral from 0 to a:
$\int_{0}^{a}{f(x)dx=}\int_{0}^{a}{f(a-x)dx}$
Integral from 0 2a
$\int_{0}^{2a}{f(x)dx=}+\int_{0}^{a}{f(2a-x)dx}$
We can also deduce that:
$\int_{0}^{2a}{f(x)dx=}2\int_{0}^{a}{f(x)dx}$ if f(2a-x)=f(2a-x)=f(x) and,
$\int_{0}^{2a}{f(x)dx=}0$ if = f(2a-x)=-f(x)
Integral from -aa
$\int_{-a}^{a}{f(x)dx=2\int_{0}^{a}{f(x)dx}}$ if f is an even function such that f(-x) = f(x)
$\int_{-a}^{a}{f(x)dx=0}$ if f is an odd function such that f(-x)= -f(x)
Constant multiples:
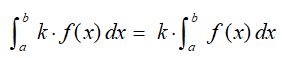
Sum and difference:
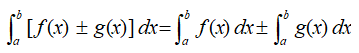
Additive Interval:
If f is integrable on the three closed intervals: a, b, and c, then we can assume that:
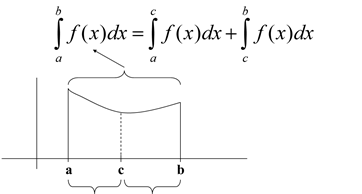
Example: Assume we know that:
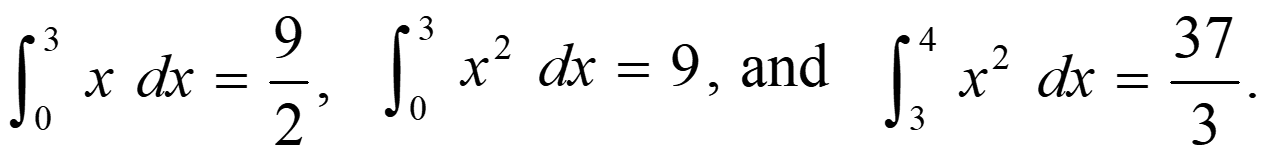
Then:
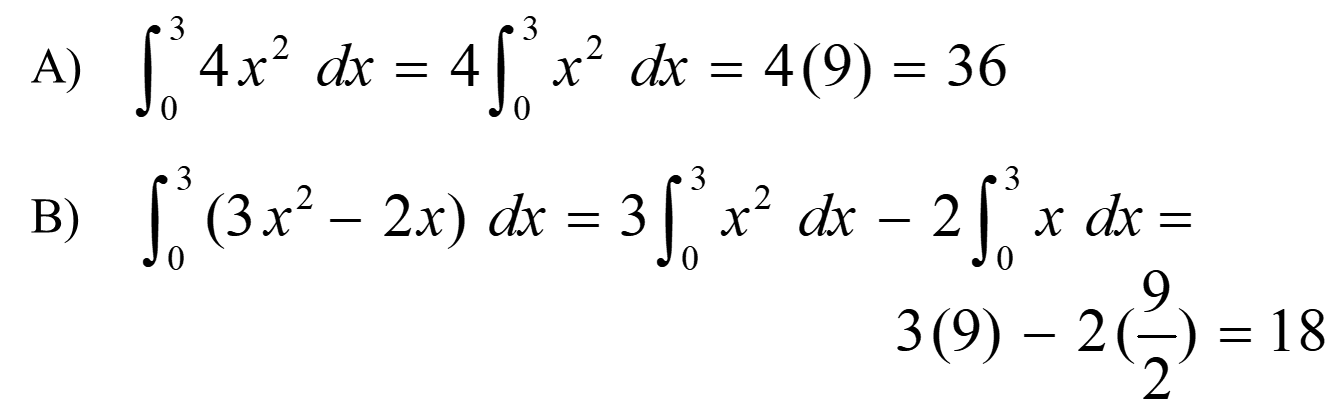
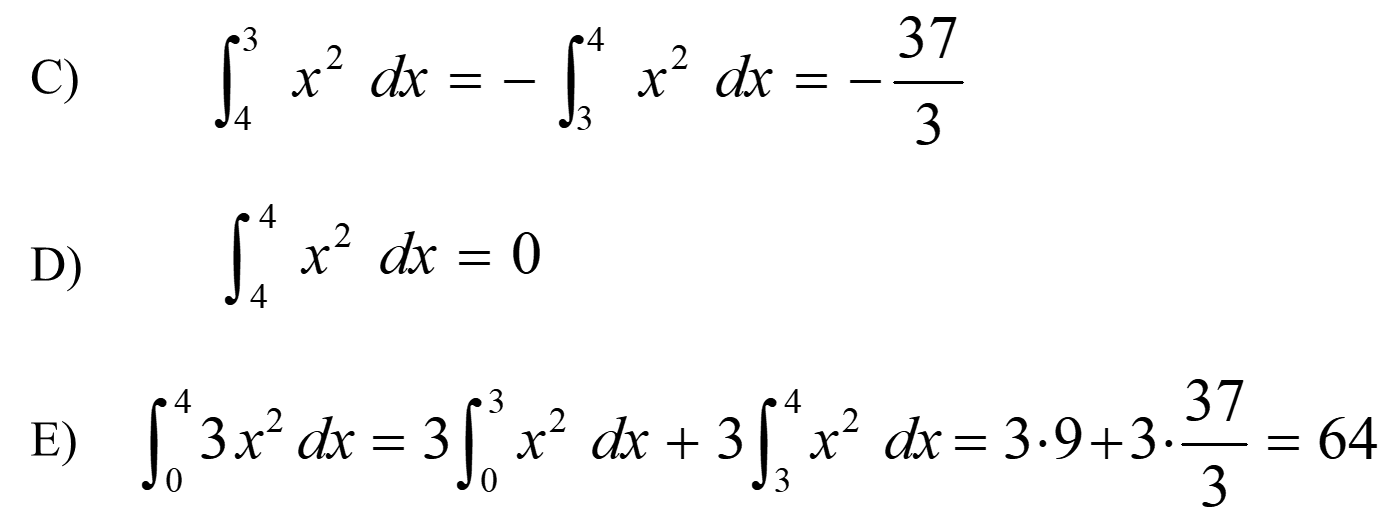
Maximum – Minimum inequality
If max f and min f are the maximum and minimum values of f on [a,b] then:
min f ∙ (b – a) ≤ $\int_{a}^{b}{f(x)dx}$ ≤ max f ∙ (b – a)
Example: Show that the value integral below is less than 3/2:
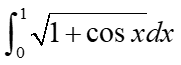
The Max-Min Inequality rule says the max f . (b – a) is an upper bound.The maximum value of the function: √(1+cosx) on closed interval: [0,1] is √2. So the upper bound is:√2(1 – 0) = √2 , which is less than 3/2
Domination: : f(x) ≥ g(x) on [a,b] , then:
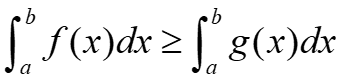
From this inequality we can deduce that f(x) ≥ 0 on closed interval [a,b] hence, $\int_{a}^{b}{f(x)dx}$ ≥ 0
Average mean value: If f is integrable on [a,b], its average (mean) value on [a,b] is:
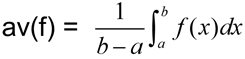
Example: Find the average value of f(x) = 4 – x2 on [0,3] . Does f portray on this value at some point in the given interval?
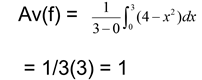
4 – x2 = 1 when x = ± √3 but only √3 falls in the interval from [0,3], so x = √3 is the place where the function assumes the average.
Mean value theorem for definite integrals:
If f is continuous on [a,b], then at some point c in closed interval:[a,b],