Potential due to an electric dipole:
Let us consider charge $-q$ is placed at point $P$ and charge $+q$ is placed at point $Q 
Figure:8.a
Electric potential at point $R$ due to electric dipole would be sum of potential due to both the charges $+q$ and $-q$. So,
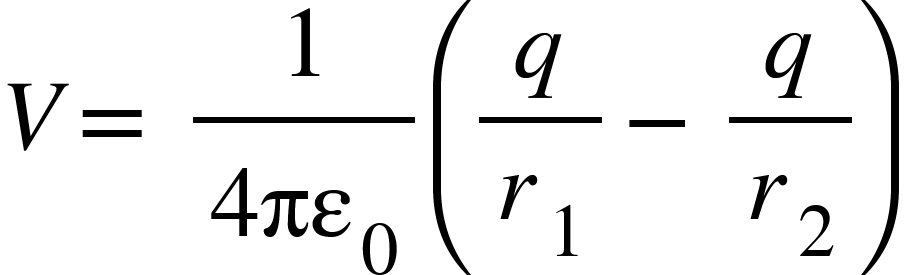………………….. (1)
Draw two perpendiculars $PC$ and $QD$from point $P$ and $Q$ as shown.
From triangle $POC$ $\cos \theta =OC/OP=OC/a$
Or, $OC=a cos\theta $
Similarly, $OD=a cos\theta $ Now,
$r_{1}=QR\approx RD=OR-OD=r-a cos\theta $
And
$r_{2}=PR\approx RC=OR+OC=r+a cos\theta $
From equation (1), we get,
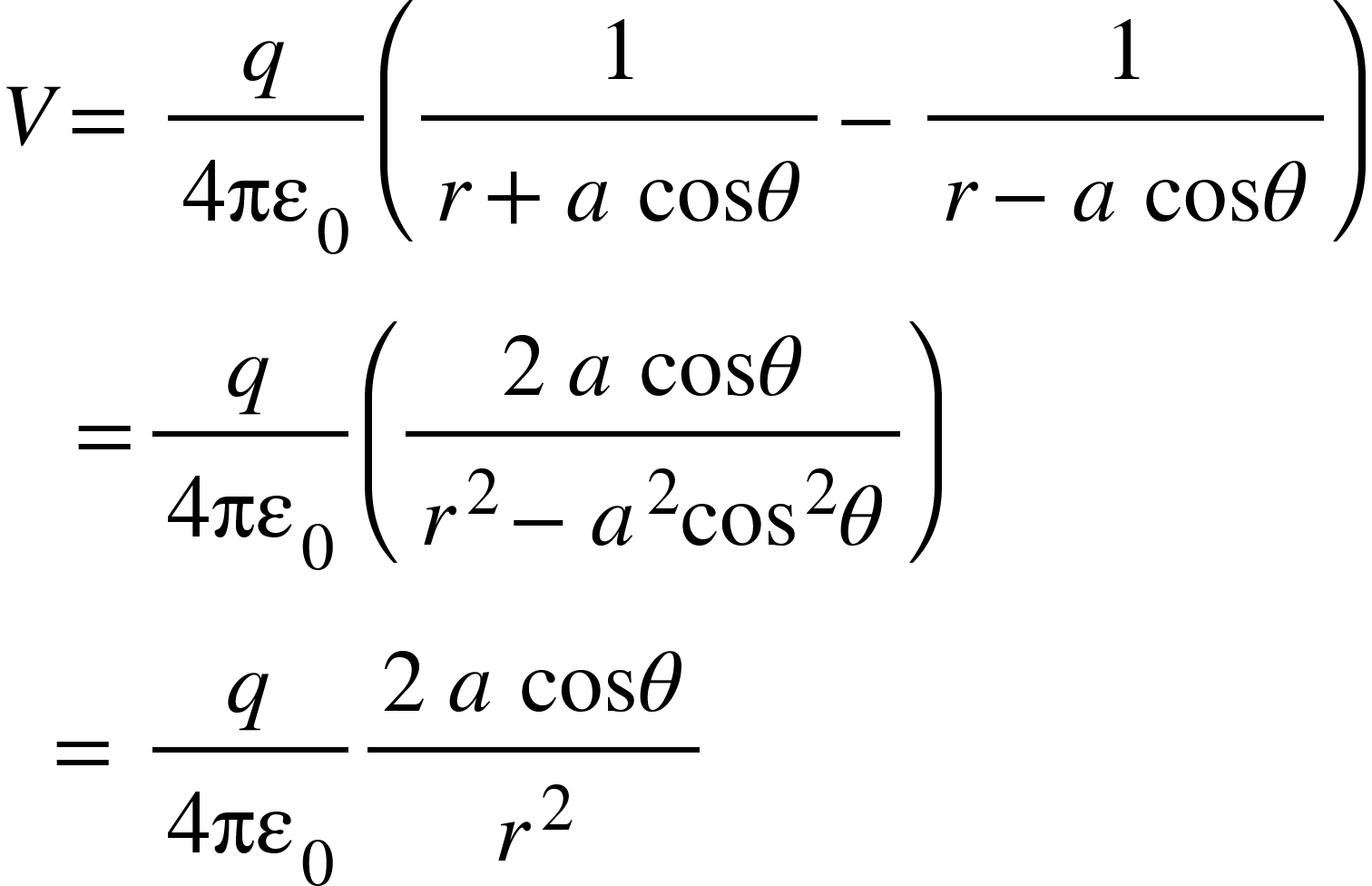
(Consider $r>>a$)
The magnitude of dipole is,$\vert p\vert =2qa$
So, the above equation becomes,
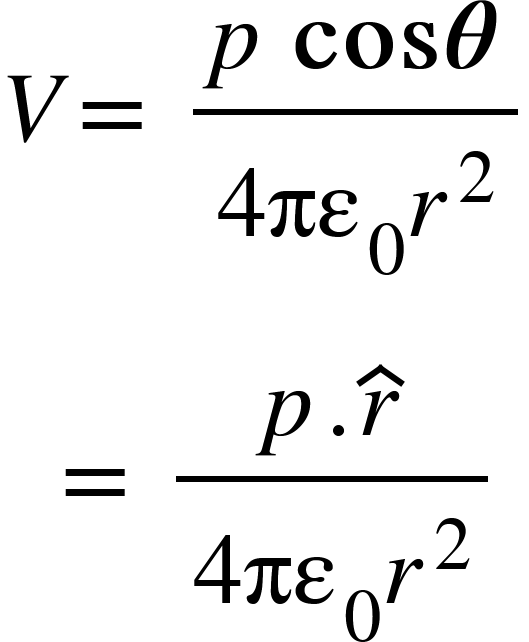
Where ${r}$ is the unit vector along the vector ${OR}$. From the above equation, we can see that the electric potential due to electric dipole does not only depend on $r$ but also depends on the angle between position vector $r$ and dipole moment $p$.
Work done in rotating an electric dipole in an electric field:
Consider a dipole placed in a uniform electric field. If the dipole is rotated from its equilibrium position, work has to be done.
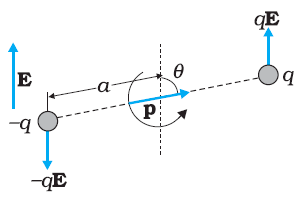
Figure:8.b
Let the dipole of the moment $p$ is rotated through an angle $\theta $ from its equilibrium position.
The torque acting on the dipole is,
$\tau =pE sin\theta $
Work done when the dipole makes a small angle $d\theta $ is given by,
$dW=pE sin\theta d\theta $ Total work done is,$W=_{0}^{\theta }{}pE sin\theta d\theta $
$W=pE\lbrack 1-cos\theta \rbrack $
This is the expression for work done in rotating an electric dipole placed in a uniform electric field $E$ through an angle $\theta $ from its equilibrium.
