Prove the identity, ![]() ?
?
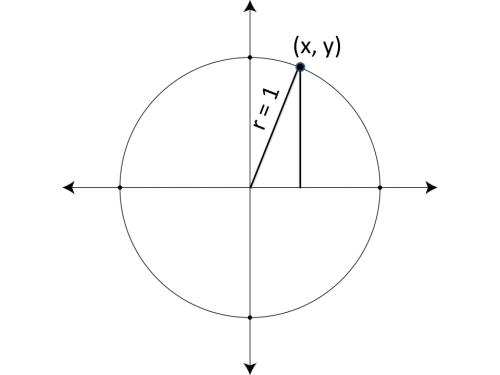
Unit Circle’s equation is x² + y² = 1
All the points on the circle contains coordinates which make the equation x² + y² = 1, true!
On the unit circle, from any arbitrary point (x, y), the representation of coordinates can be given by (sin ![]() + cos
+ cos ![]() ), where,
), where, ![]() is rotation’s degree from the x-axis which is positive.
is rotation’s degree from the x-axis which is positive.
On substitution, sin ![]() = x & cos
= x & cos ![]() = y into the unit circle’s equation, thus, we can observe that sin
= y into the unit circle’s equation, thus, we can observe that sin ![]() ² + cos
² + cos ![]() ² = 1.
² = 1.
Generally, the identity given is just proven with the help of the Pythagoras theorem and the unit circle, either range of different methods or calculus.
Although if one proves it with the help of different methods, it’s important to remember that we can’t prove all the trigonometric identities with the use of alternative trigonometric identities, as that would be depending on a circular reasoning, in addition to that even if we prove it using different trigonometric identities, we should be using different methods in some or the other way.
It so appears that sin²(x)+cos²(x)=1 is known to be one of the simpler identities to verify with the use of alternative methods, and therefore, it’s usually done in this way.
Nevertheless, let’s now switch on to the proof with the formula of angle addition use for cosine:
cos(α + β)= cos(α)cos(β)−sin(α)sin(β)
Further, it’s important to note that odd function is sine and the even function is cosine, which means,
sin(−x) = −sin(x);
cos(−x) = cos(x)
Now, proceeding for the proof:
Let α = x; β = −x
Cos ( x + (-x)) = Cos (x) Cos (-x) – Sin (x) Sin (-x) ⇒ Cos (0) = cos (x) cos ( x – (-sin (x) sin (x)) …………………………eq.1
Considering the above equation
sin(−θ)= −sin(θ)
cos(−θ) = cos(θ)
Therefore, 1 = cos²(x) + sin²(x)
Another simplest method to prove this identity is:
Proof:
Let’s consider the right angled triangle, having θ as the internal angle:
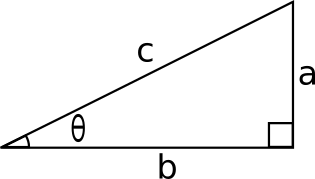
Then: sinθ= a / c,
cosθ =b / c
Therefore,
sin²θ + cos²θ = a² / c² + b² / c² = a² + b² / c²
By the Pythagoras theorem:
As a² + b² = c²,
Accordingly, a² + b² / c² = 1 ; (a² + b² – c² = 0)
So, by the given Pythagoras, which proves this identity for
θ∈ (0, π / 2) or (0, 90º)
For angles that are present outside this range then, we can make use of:
- sin(−θ)= −sin(θ)
- Sin (θ+π) = −sin(θ)
- cos(−θ) = cos(θ)
- cos(θ+π) = −cos(θ)
Hence, for eg:
sin²(θ+π) + cos²(θ+π) = (−sinθ)² + (−cosθ)² = sin²θ + cos²θ = 1
Or,
sin²(θ+180º) + cos²(θ+180º) = (−sinθ)² + (−cosθ)² = sin²θ + cos²θ = 1
Considering Pythagoras theorem
In a right angle triangle given having a, b, and c as their sides
So, consider this below diagram:
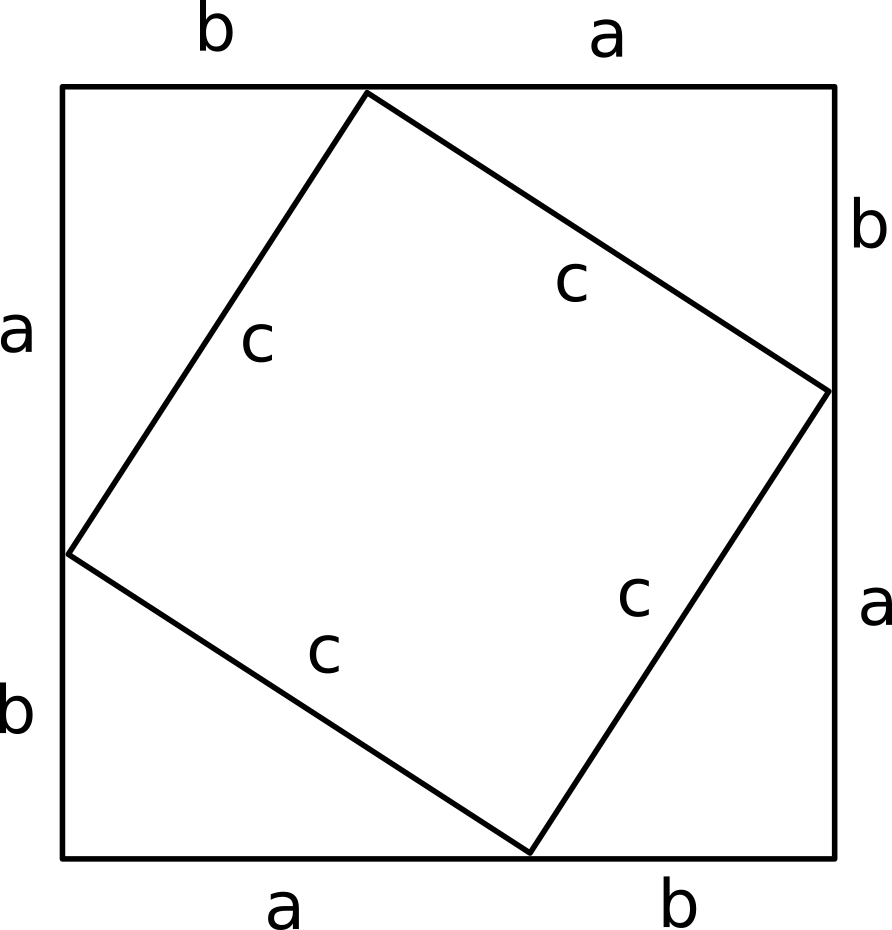
Area of larger square = (a+b)²
Area of smaller square is = c²
Area of each triangle = 1 / 2 a.b
Therefore, we have:
(a+b)² = c² + 4 ⋅ 1 / 2 a*b ; i.e.
a² + 2ab + b² = c² + 2ab
Now,
From both sides, subtract “2a” to get:
a²+ b² = c2