Diffraction Due to ASingle Slit, Width of Central Maximum
The single slit diffraction can be observed when the light is passing through the single slit, which is having a width in the order of light’s wavelength. On the screen, the diffraction pattern will be at a distance L away from the slit. Here the intensity is considered as a function of the angle.
Single Slit Diffraction
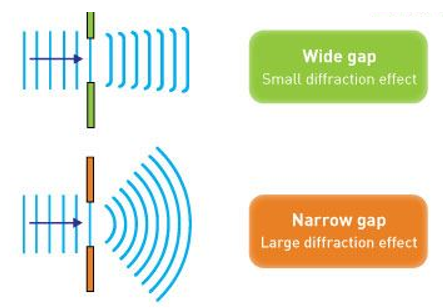
In the single-slit diffraction experiment, as shown above, the diffraction or bending phenomenon of light can be observed, which is causing the light from the coherent source to interfere with itself and causes the production of distinctive patterns on the screen known as the diffraction pattern. The diffraction can only be evident when the light sources are small enough that their size is relative to the wavelength of light. This effect can also be observed in the above diagram. For the larger slits, the spreading is unnoticeable as it is extremely small.
When the light is passing through the single slit that is having the width w, and it is in the same order of the light’s wavelength, then the single slit diffraction is observed at the distance L from the slit. According to Huygens’s principle, all parts of the slit can be considered as emitting sources of the waves. All of these waves are interfering with producing the diffraction pattern. The constructive interface is observed by the meeting of crests with the crests and destructive interface is formed when the crest is meeting trough.
At a point far from the source, the wavefronts are essentially plane waves. This point is known as the Fraunhofer regime, and the observed diffraction pattern is known as Fraunhofer diffraction. The position of all the minima (destructive interfaces), and maxima (constructive interfaces) can be easily calculated.
Central Maximum
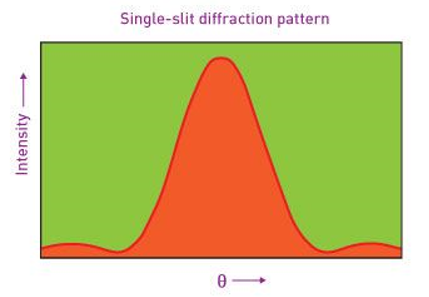
The maxima lie between the width of central maximum and minima. It is the distance between the first order minima, from the center of the screen to both sides of the center. By considering the position of minima,
sin θ≈θ
⇒ λ = a sin θ≈aθ
⇒ θ = yD = λa
⇒ y = λDa
The value of the width of the central maximum is twice than this value. The width of the central maximum can be written as follows
= 2λDa
Whereas, the angular width of the central maximum,
= 2θ = 2λa
The intensity graph and the refraction pattern can be shown in the below diagram.