The square root of x is the number r in a way that r² = x. When represented in ![]() form or specifically,
form or specifically, ![]() , the square root of x might also be known as the surd or radical. Therefore, the square root is the nth root, having the value, n = 2.
, the square root of x might also be known as the surd or radical. Therefore, the square root is the nth root, having the value, n = 2.
It’s the point of notice that any real number which is positive contains 2 square roots in which one is positive and the other one is negative. Let’s say, the 16 is having square root as +4 & -4, since (-4)² = (+4)² = 16.
Any real number having non-negative value, x contains a unique square root which is non-negative which is ‘r’; and this is known as the principal square root & is written as, ![]() or
or ![]() .
.
Let’s say, the principal square root of 16 is √16 = +4, while the alternative sq. root of 16 = -√16 = -4. In general use, however, specified, the square root is usually taken into action which means as the “principal square root”. The function of the principal square root ![]() is
is ![]() ’s inverse function for the value,
’s inverse function for the value, ![]() .
.
To Determine The Square Root Of The Complex Number a + ib
Where a &*b (≠0) are real values
Assuming √a + ib = x + iy, where value of x & y are for real.
Then, a + ib = (x + iy)2 = x2 + i2y2 + 2x * iy = x2 – y2 + i *2xy ∵ (a +b)² = a² + 2ab + b²
Now, on equating both imaginary and real parts, we have,
x2 – y2 = a Eq. 1
2xy = b Eq. 2
Now, (x2 + y2)2 = (x2 – y2)2 + 4x2y2 = a2 + b2
Therefore, x2 + y2 = +√a2 + b2 (∵ x, y are both real) Eq. 3
Now, on the addition of equations – (1) and (3) we get,
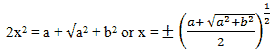
Now equation (3) – equation (1) gives,
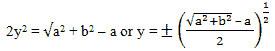
So, from the 2nd equation, it’s pretty much understandable that both the values of x & y consist of the same signs which can either be both +ve or both -ve.
When b holds the +ve value, and the values x & y encompasses two different signs, namely as the positive one and the other as the negative one. when b holds -ve value.
Therefore, if b > 0 then, as a result, you’ll see that the square roots of (a + ib) will be equal to:
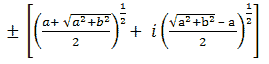
In the condition when b < 0, therefore, the square root value of (a + ib) will be in the form:
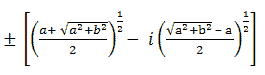
For further explanation, see a few of the examples:
Example 1:
Find the square root of 4 – 3i
Solution:
Let z² = (x + yi)2 = 4 – 3i
Therefore, (x2 – y2) + 2xyi = 4 – 3i
On comparison of real & imaginary parts,
x2 – y2 = 4 Eq. 1
2xy = -3 Eq. 2
Now, considering the modulus: |z|2 = |z2|
x2 + y2 = Ö(42 + 32) = 5 Eq. 3
On solving the two equations i.e. Eq 1 and Eq 3, we get,
x2 = 2; y2 = ½
Thus, x = ±√2; y = ±√1/2
So, from equation 2, x & y contains opposite signs
(x=√2 ; y = -√1/2) & (x = -√2 ; y = √1/2)
Hence, z = ±(√2 – √1/2i)