Straight Lines: General equation of a line

by

Linear equations contain two variables and when we plot all the (x,y) pairs that make the equation for a line.

The formula for Standard Form is:

Here, A, B and C are real numbers and A≠ and B≠0.

Since the slope of a vertical line is undefined we don’t write the equation of a vertical line using either the slope-intersect form or the point-slope form. But we can use the standard form to express vertical lines.

To find where the line crosses each axis, let the other value be zero.

  • If y is zero, we have Ax = C, C/A is the x-intercept.
  • If x is zero, we have By = C, C/B is the y-intercept.
  • − A/B is the slope.

Using the x-intercept and/or y-intercept as a starting point, you can use the slope to graph more points on the line of the equation.

Write an equation of the line in STANDARD/GENERAL FORM using the information given: m=2 and (3, -2)

Start with Point-Slope Form

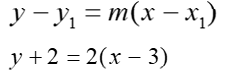
Now put into slope-intercept form

Now put into the general form:

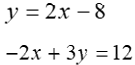
Leading negatives are not recommended. Therefore, change all the signs of each term

Write an equation of the line in STANDARD FORM using the information given: (-4, 4) and (0, 3)

Start with Point-Slope Form

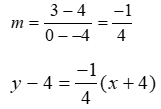
Now put into slope-intercept form

Now put into Standard form

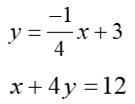
The process of simplifying any type of line equations to the general form is as follows:

  1. Do all the possible algebraic operations ( multiplication division addition and subtraction)
  2.  Find the determinant in case of  two-point form
  3.  evaluate all the trigonometric ratios in the case of normal form
  4.  eliminate the parameter in case of two intercept form and slope-intercept form
  5.  shift all the gums on one side of the equation
  6.  Arrange the terms by algebraic operations and present them in this style
Equation form Equation Notes
Slope-intercept y = mx + b m is the slope.

b is the y-intercept.
Point slope m is the slope and (x1, y1) is a point on the line
Normal form p is the perpendicular from the origin to the line and α is the angle between this perpendicular and the x-axis.
Intercept form a= x-intercept and b= y-intercept
Parallel to axis Vertical: x=a and Horizontal y=b a= x-intercept and b= y-intercept
Two-point form The line passes through A (x1, y1) and B (x2, y2)
Standard form A is positive. A, B and C are real numbers and A≠ and B≠0.