Consistency, inconsistency and number of solutions of a system of linear equations by examples, solving system of linear equations in two or three variables using the inverse of a matrix
A linear equation multiple variables: x, y, z etc. is an equation of the form: ax + by + cz = p, where a, b, c (not all zero) and p are constants.
Let us show the system of linear equations as matrix equations and then use the inverse matrix of the coefficient matrix to solve them. Consider the system of equations:

Let A be a non-singular matrix, this means that its inverse also exists. If the determinant is nonzero, the equation can be solved to produce n numerical values for x that satisfy all the simultaneous equations. To solve, premultiply both sides of the equation by A-1 which exists because of|A| = 0
The solution to a linear system of equations is then given by:
$AX=B$
$A^{-1}(AX)=A^{-1}B$
$(A^{-1}A)X=A^{-1}B$
$IX=A^{-1}B$
$X=A^{-1}B$
Since the inverse of a matrix is unique, the matrix equation above provides a unique solution. So if the inverse of the coefficient matrix is found, the unknowns, X would be determined.
Example:
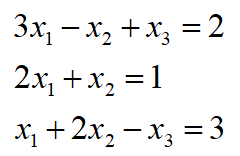
The equation can also be written as:
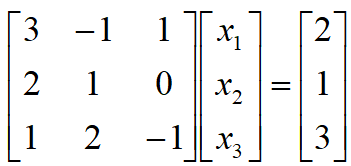
Using the inverse we obtain:
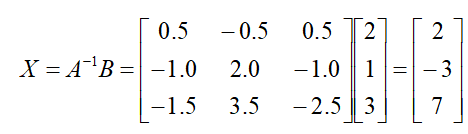
Hence,
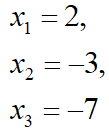
The values for the unknowns should be checked by substitution back into the initial equations
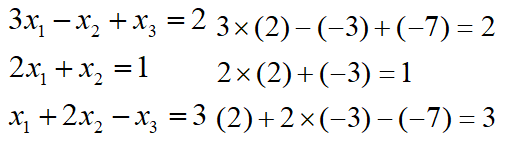
Example: Use matrices to solve the simultaneous equations below.
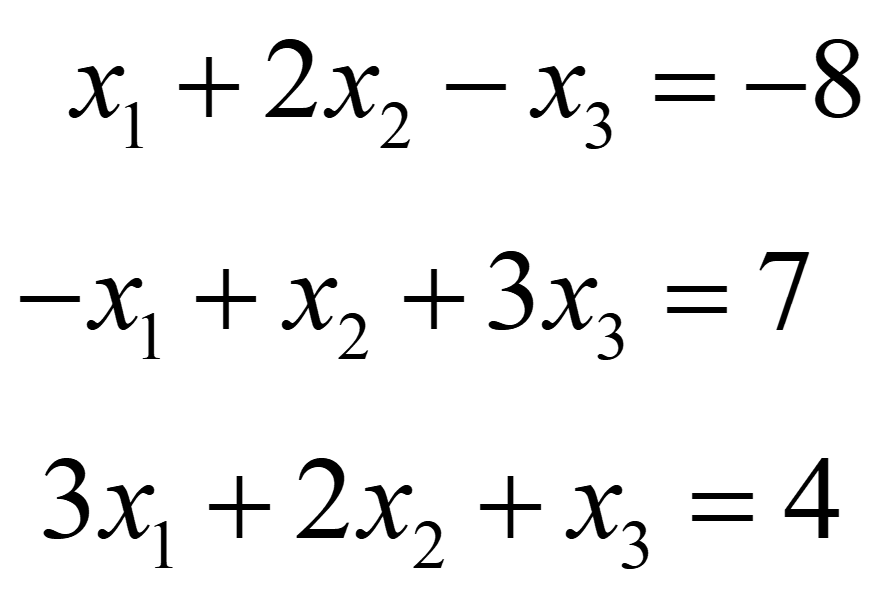
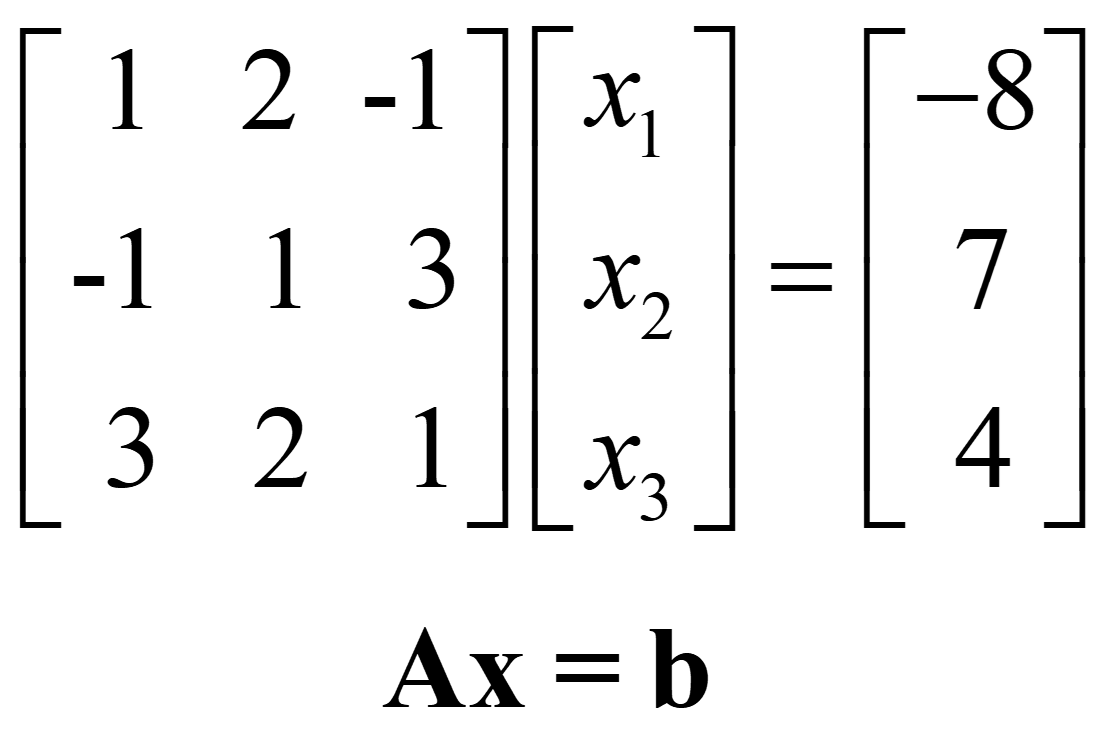
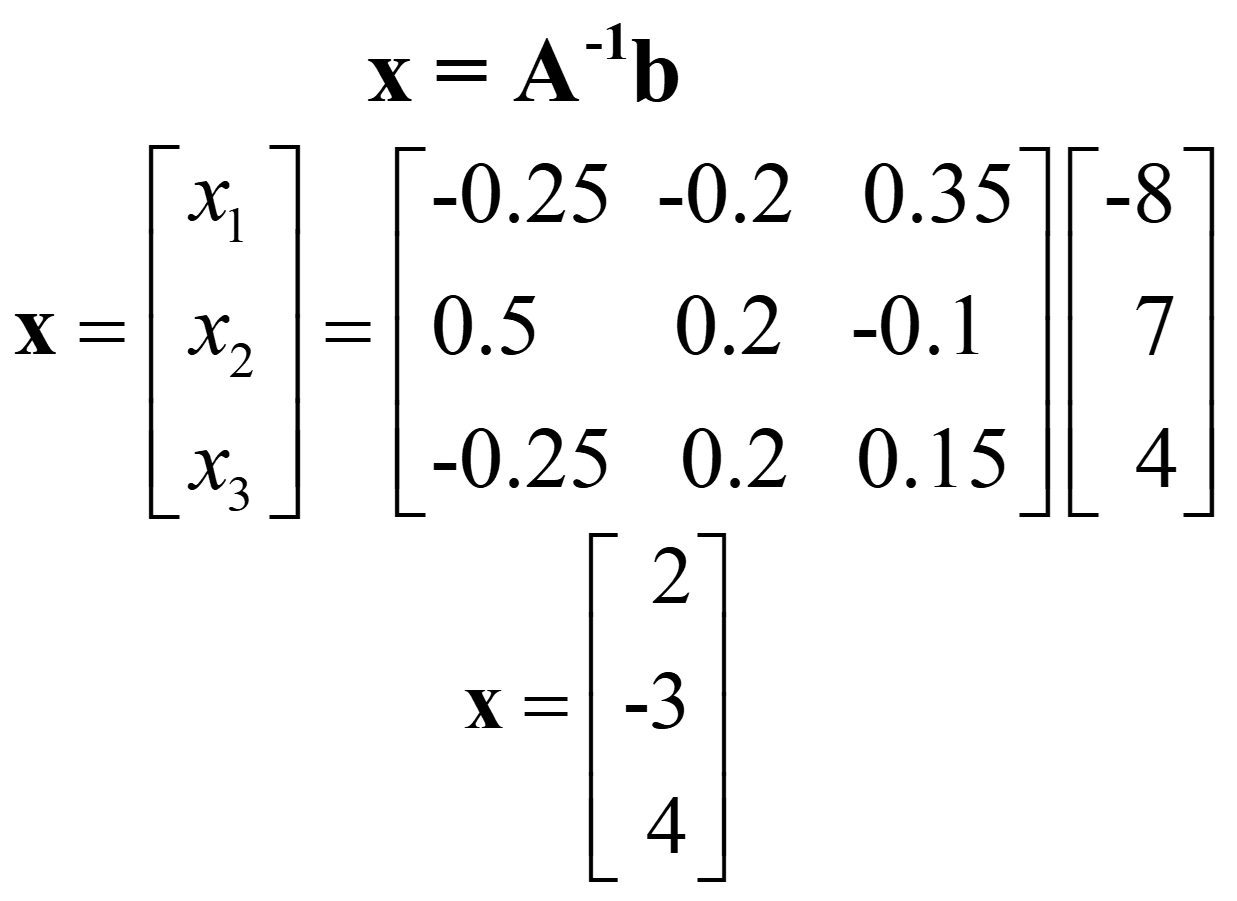
Let A be a singular matrix, then we know that . If (adj A)B≠ 0, where 0 is a zero matrix then the system of equation is considered inconsistent. If (adj A)B = 0, the system of equations may or may not be consistent as it can either have infinitely many solutions or no solution.
Now consider the following example:
You have 10,000 rupees to invest. You want to invest the money in a stock mutual fund, a bond mutual fund, and a money market fund. The expected annual returns for these funds are given in the table.
The expected overall annual return on the investment is 8%. A financial planner recommends that you invest the same amount in stocks as in bonds and the money market combined. How much should you invest in each fund?
We can form three equations from the given information:
These linear equations can then be written in matrix form:
Now, to isolate the variable matrix, RIGHT multiply by the inverse of A. Recall that X = A-1 B
$A^{-1}=\lbrack \begin{matrix}
0.5 & 0 & 0.5 & \\
-3.75 & 50 & -1.25 & \\
4.25 & -50 & 0.75 & \\
\end{matrix}
\rbrack $\\
$\lbrack \begin{matrix}
s & \\
b & \\
m & \\
\end{matrix}
\rbrack =\lbrack \begin{matrix}
0.5 & 0 & 0.5 & \\
-3.75 & 50 & -1.25 & \\
4.25 & -50 & 0.75 & \\
\end{matrix}
\rbrack \lbrack \begin{matrix}
10000 & \\
800 & \\
0 & \\
\end{matrix}
\rbrack $\\
$\lbrack \begin{matrix}
s & \\
b & \\
m & \\
\end{matrix}
\rbrack =\lbrack \begin{matrix}
(0.5\times 10000)+0+0) & \\
(-3.75\times 10000)+(50\times 800)+0 & \\
(4.25\times 10000)+(-50\times 800)+0 & \\
\end{matrix}
\rbrack =\lbrack \begin{matrix}
5000 & \\
2500 & \\
2500 & \\
\end{matrix}
\rbrack $