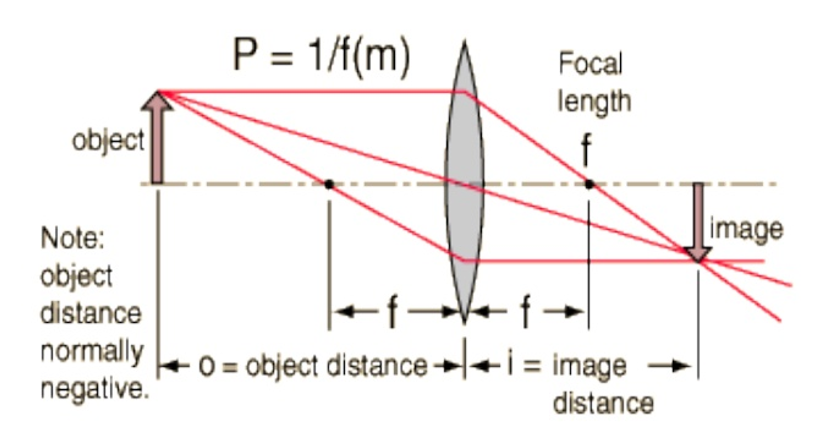
The equation relating to the distance of the object, focal length, and distance of image is known as lens formula. A common Gaussian form of thin lens formula is given below. The cartesian sign convention is also used due to its advantages with the more complex optical instruments and multiple lens systems. Both these forms can be used with the negative and positive lenses, for the prediction of the formation of both inverted and real images. Thin lens formula is only valid for the paraxial rays which are closer to the optical axis, and this formula cannot be applied to the thick lenses.
How to Use Thin Lens Formula
The lens whose thickness is negligible, in comparison to its radius of curvature, then it can be categorized as a thin lens. When the focal length of the lens is known, then it can be used for finding a relationship between the distance of the image and distance of the object. The value of (1/u + 1/v) is constant and its value is equal to 1/f. In this way, the relationship between the image distance, object distance, and focal length of a thin lens can be given by the formula as shown below. This formula can be applied to both concave lenses and convex lenses.

In the figure, shown above f is representing the focal length, v shows the distance between the image and optical center, and u denotes the distance between the object and optical center. If the focal length is negative, then it is the implication that the lens is concave or diverging. But if the focal length is positive, then it shows that the lens is convex or converging. If the calculated distance of the image is negative, then it shows the formed image is virtual and it is formed on the same side as of the object. It is also possible to calculate the magnification of the image by using the following formula.
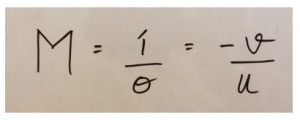
Here v is the height of the object, u is the height of the image. If i is positive, then the direction of the image is upright, and if the calculated value of i is negative then it means that the image is inverted. The two formulas, given above can be together referred to as lens formula.
Assumptions for Thin Lens Formula
- The aperture of the lens is small.
- The incident rays are making small angles with the surface of the lens on the principal axis.
- The lens is not thick.
- The object is lying close to the principal axis.