We need at least two points to determine the nature of a line. This analogy is used to quickly sketch a line if its equation is given in the Two Intercept-Form. Consider the following graph where a line L makes x-intercept at a and y-intercept at b on the axes. This means that L meets x-axis at the point (a, 0) and y-axis at the point (0, b).
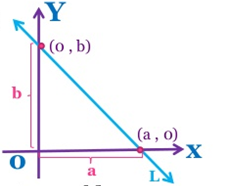
Use the two-point form of the equation to substitute the values of the intercepts:
$y-y_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}(x-x_{1})$
$y-0=\frac{b-0}{0-a}(x-a)$
$y=\frac{-b}{a}(x-a)$
$\frac{y}{b}=\frac{-(x-a)}{a}$
$\frac{y}{b}=\frac{-x}{a}+\frac{a}{a}$
$\frac{x}{a}+\frac{y}{b}=1$
$\frac{x}{a}+\frac{y}{b}=1$
Again, a= x-intercept and b= y-intercept
To convert the equation into a slope-intercept form may y as the subject:
$\frac{x}{a}+\frac{y}{b}=1$
$\frac{y}{b}=1-\frac{x}{a}$
$\frac{y}{b}=\frac{a-x}{a}$
$y=\frac{b(a-x)}{a}$
$y=\frac{ba}{a}-\frac{x}{a}$
$y=-\frac{1}{a}x+\frac{ba}{a}$
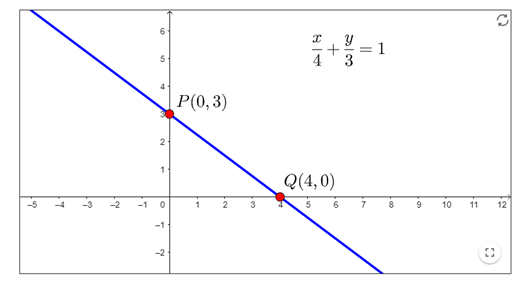
Example 1. Determine the equation of the line with x-intercept 4 and y-intercept 3.
x-intercept a = 4.
y-intercept b = 9.
Substitute in the formula as
$\frac{x}{a}+\frac{y}{b}=1$
$\frac{x}{4}+\frac{y}{3}=1$
Example 2. Find the equation of a straight line with X-intercept A(-7,0) and Y-intercept B(0,14).
From the above information, we know the X-intercept is a=-7 and the Y-intercept is b=14. Now we substitute the values in the formula of the intercepts form as given:
$\frac{x}{a}+\frac{y}{b}=1$
$\frac{x}{-7}+\frac{y}{14}=1$
$\frac{2x-y}{-14}=1$
$2x-y=-14$
$2x-y+14=0$
Example 3. Convert general form of the equation into intercept form for 9x-5y=4
Let x=0 find y-intercept:
$9(0)-5y=4$
$-5y=4$
$y=-\frac{4}{5}$
Let y = 0 to find x-intercept:
$9(x)-5(0)=4$
$9x=4$
$x=\frac{4}{9}$
Substitute the values in the two-intercept form:
$\frac{x}{a}+\frac{y}{b}=1$
$\frac{x}{4/9}+\frac{y}{-4/5}=1$
Example 4. Reduce the general equation -8x+5y = 9 into intercept form and find the x-intercept and y-intercept.
$-8x+5y=9$
First, divide both sides by 9
$\frac{-8x}{9}+\frac{5y}{9}=1$
Now bring the x and y coefficient to the denominator:
$\frac{x}{9/-8}+\frac{y}{9/5}=1$
Example 5. Find the x- and y-intercepts of the line using these coordinates, (–4, –5) and (6, 2).
Convert the points to intercept form equation by:
| Using slope-intercept form | Using two-point form |
| y = mx + b | $\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}$ |
| Find m$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{2+5}{6+4}=\frac{7}{10}$ | Substitute the values of an ordered pair to form general equation: $ \frac{y+5}{2+5}=\frac{x+4}{6+4}$ $\frac{y+5}{7}=\frac{x+4}{10}$ $10(y+5)=7(x+4)$ $10y+50=7x+28$ $10y-7x+22=0$ |
| Substitute (6, 2 ) in the slope-intercept form to obtain y-intercept:$ 2=\frac{7(6)}{10}+b$ $2-\frac{42}{10}=b$ $-\frac{22}{10}=b$ b = -22/10 |
Convert the general equation into intercept form:$ \frac{10y}{22}-\frac{7x}{22}+1=0$ $\frac{10y}{22}-\frac{7x}{22}=-1$ $\frac{-10y}{22}+\frac{7x}{22}=1$ |
| Substitute m and b to find x intercept when y=0$y=mx+b$ $0=\frac{7}{10}x-\frac{22}{10}$ $\frac{7}{10}x=\frac{22}{10}$ $x=\frac{22}{10}\cdot \frac{10}{7}$ $x=22/7$ a = -22/7 |
Shift the coefficient of x and y to the denominators:$ \frac{-10y}{22}+\frac{7x}{22}=1$ $\frac{y}{22/-10}+\frac{x}{22/7}=1$ a=22/7 and b=-22/10 |
| Substitute the values of a and b in the intercept form:$ \frac{-10y}{22}+\frac{7x}{22}=1$ |
The equation is written as:$\frac{-10y}{22}+\frac{7x}{22}=1$ |