Equal vectors: Vectors with the same length and direction, and must represent the same quantity (such as force or velocity).
Unit vector: For this vector, the length is always 1.For a vector 𝑎 ⃗ , a unit vector is in the
the same direction as 𝑎 ⃗ and is given by: ${a} = \frac{\overrightarrow{a}}{\vert \overrightarrow{a}\vert }$
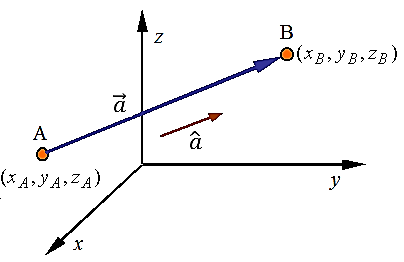
$\begin{matrix}
a_{x}=(x_{B}-x_{A}) & \\
a_{y}=(y_{B}-y_{A}) & \\
a_{z}=(z_{B}-z_{A}) & \\
\end{matrix}
$
${a} = \frac{a_{x}{i} + a_{y}{j} + a_{z}{k}}{\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}=\frac{1}{\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} (\begin{matrix}
a_{x} & \\
a_{y} & \\
a_{z} & \\
\end{matrix}
)$
Zero vector: When the initial and terminal points of the vector coincide, we obtain a zero vector or null vector and it is denoted as $\overrightarrow{0}$. For example, $\overrightarrow{AA}$ or $\overrightarrow{PP}$ represents a zero vector.
Parallel vectors:
$\overrightarrow{a}$ is parallel to $\overrightarrow{b} ⇔ \overrightarrow{a}= k\overrightarrow{b}k\epsilon R$
$\overrightarrow{a}= (\begin{matrix}
6 & \\
9 & \\
3 & \\
\end{matrix}
) \overrightarrow{b}= (\begin{matrix}
2 & \\
3 & \\
1 & \\
\end{matrix}
) (\begin{matrix}
6 & \\
9 & \\
3 & \\
\end{matrix}
) = 3(\begin{matrix}
2 & \\
3 & \\
1 & \\
\end{matrix}
) \to \overrightarrow{a} || \overrightarrow{b}$
Coinitial vectors:
Two or more vectors that have the same initial points are called coinitial vectors. Eg. $\overrightarrow{AB }$ and $\overrightarrow{AC}$ are coinitial vectors.
Collinear vectors:
Points are collinear if they lie on the same line. A, B and C are collinear ⇔ $\overrightarrow{AB}=k\overrightarrow{AC}$ for some scalar k. This means that they have one common point and in the same direction.
Example: Show that P(0, 2, 4), Q(10, 0, 0) and R(5, 1, 2) are collinear.
$ \overrightarrow{PR}=(\begin{matrix}
5 & \\
-1 & \\
-2 & \\
\end{matrix}
), \overrightarrow{QR}= (\begin{matrix}
-5 & \\
1 & \\
2 & \\
\end{matrix}
) \overrightarrow{QR}= -1\times \overrightarrow{PR}
$
$\overrightarrow{QR}$ and $\overrightarrow{PR}$ have a common direction and a common point. Therefore P, Q, and R are collinear.
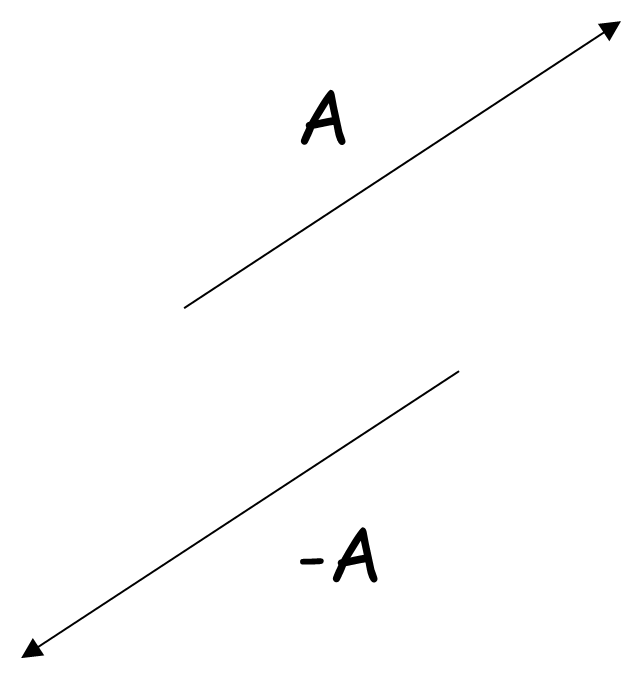
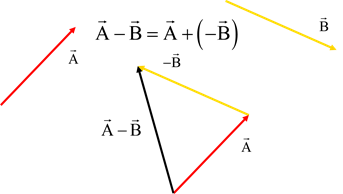
Negative of a vector:
Negative of a vector or Inverse vectors have the same length, but opposite direction.
Vector Addition:
The sum of two or more vectors = resultant vector. The resultant vector can replace the vectors from which it is obtained. It is completely canceled out by adding it to its inverse, which is then called the equilibrant.
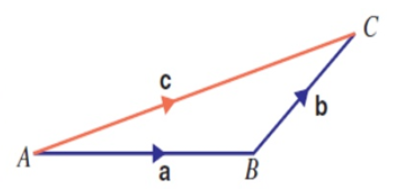
Triangle Law:
Let $\overrightarrow{AB}$ represent a vector a and $\overrightarrow{BC}$ represent a vector b. Then $\overrightarrow{AC}$ represents the vector c in the triangle shown below:
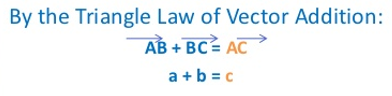

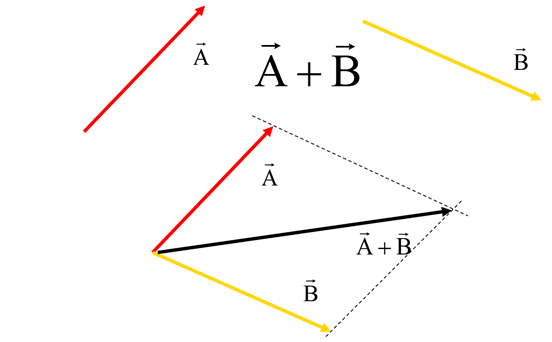
Parallelogram law:
Arrange the tail of the vector to tail in the correct direction and draw to scale. Now sketch two identical vectors as the originals to form a parallelogram. Draw in the diagonal of the parallelogram. This is your answer called a resultant. Measure the resultant and find the angle.
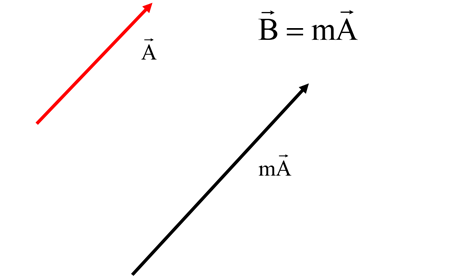
Vector multiplication with scalar: Let $\overrightarrow{a}$ and $\overrightarrow{b}$be two vectors and g and h as the scalar quantity. Then we can assume that:
- $g\overrightarrow{a}+h\overrightarrow{a} =(g+h)\overrightarrow{a}$
- $g(h\overrightarrow{a})=(gh)\overrightarrow{a}$
- $g(\overrightarrow{a} +\overrightarrow{b})=g\overrightarrow{a} +g\overrightarrow{b}$
Properties of vectors:
1. Commutative Property: A+B = B+A
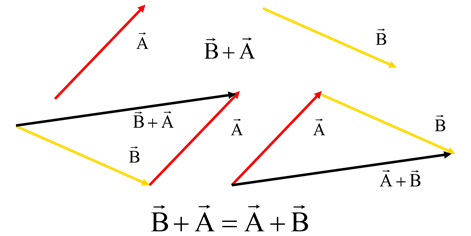
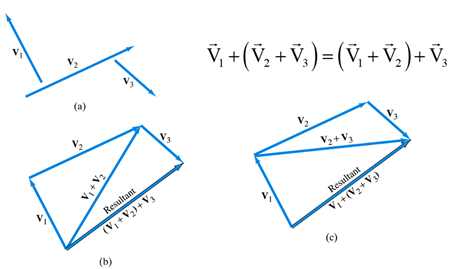
2. Associative Property: (A+B)+C = A+(B+C)
3. Zero Property: A+(-B) = 0, iff, A has the same magnitude to B and pointing in the opposite direction.
4. Subtraction: A – B = A + (-B)
5. Multiplication: 3 x A = 3A
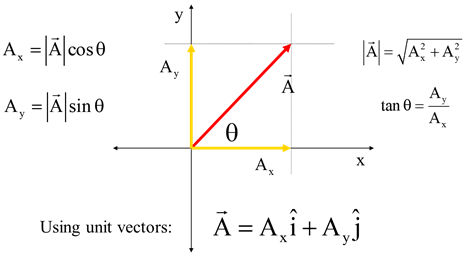
Components of a vector: In three dimensions, the vector components of vector A are three perpendicular vectors AxAyand Az that are parallel to the x, y and z axes, respectively, and add together vectorially so that
A = Ax + Ay + Az
In this case: Ax = A cos Qx, Ay = A Sin Qy and Az = A Tan Qz
The position vector of a point that divides a line segment in a given ratio:
Let the point on line segment AB :A = (2, 7, 8) B = ( 2, 3, 12)
X divides [AB]in the ratio means $\overrightarrow{AX}:\overrightarrow{XB}=a :b$
Example: P divides [AB] internally in ratio 1:3. Find P
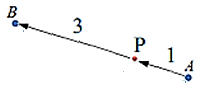
$\overrightarrow{AP}:\overrightarrow{PB}=1:3 \to \overrightarrow{AP}=\frac{1}{4} \overrightarrow{AB}$
$\overrightarrow{AP}=\frac{1}{4} \overrightarrow{AB}$
$(\begin{matrix}
x-2 & \\
y-7 & \\
z-8 & \\
\end{matrix}
)=\frac{1}{4}(\begin{matrix}
0 & \\
-4 & \\
4 & \\
\end{matrix}
)$
point P is (2, 6, 9)
Example: X divide [AB] externally in ratio 2:1, or X divide [AB] in ratio –2:1. Find Q
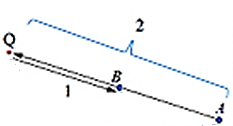
$\overrightarrow{AQ}:\overrightarrow{QB}=-2:1$
$\overrightarrow{BQ}=\overrightarrow{AB}$
$(\begin{matrix}
x-2 & \\
y-3 & \\
z-12 & \\
\end{matrix}
)=(\begin{matrix}
0 & \\
-4 & \\
4 & \\
\end{matrix}
)$
point Q is (2,– 1,16)