Relationship between the temperature of a black body and also the wavelength at which it emits the most light, Wein’s displacement law was named after German scientist Wilhelm Wien, who received the award for Physics in 1911 for discovering the law.
Wien studied the wavelength or distribution of black-body radiation within the 1890s. It was his idea to use as a good approximation for the ideal blackbody an oven with a small hole. Anyone of the radiation that enters into the tiny hole is scattered here and there and then reflected from the inner walls of the oven thus usually that nearly all incoming radiation is absorbed and therefore the chance of some of it finding its way out of the hole again can be made exceedingly small. The radiation coming out of this hole is then very close to the equilibrium blackbody electromagnetic radiation corresponding to the oven temperature. Wien found that the radiative energy per wavelength interval dλ features a maximum at a particular wavelength λm and that the maximum shifts to shorter wavelengths because the temperature T is increased. He discovered that the product λmT is a perfect constant: λmT = 0.2898 centimeter-degree Kelvin.
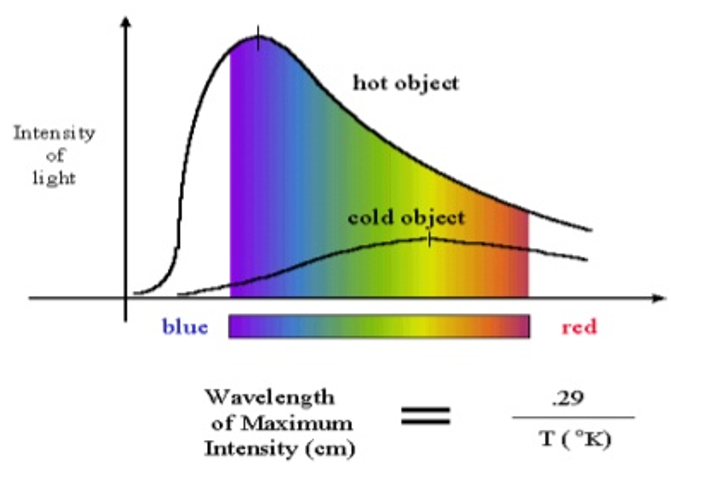
Another quantity of interest, which relates to the black-body radiation spectrum, is the wavelength: λm, to which corresponds the maximum of surface density of an emitted energy flux.This maximum displaces to the side of shorter wavelengths as the temperature increases. Quantity λm can be found by differentiating the Planck function from equation and by equating the obtained expression to zero. As a result, the transcendental equation is obtained
1 \
λmT = C2 /5 1 — exp (—C2/ λmT)
Whose solution is as follows„
λmT = C3 and represents one of the expressions of the Wien displacement law. According to the equation, as the temperature increases, the maxima of the surface density of the radiation flux and its intensity displace to the side of shorter wavelengths in inverse proportion to Z. If we consider the black-body radiation into a transparent medium (with refractive index n), then the Wien law takes the form of
nλm, nT = C3,
Whereλm, n is the wavelength corresponding to the maximum of radiation in the transparent medium.
Of interest is the fact that the substitution of the wavelength from the Wien displacement law into equation results in the following expression„
I λ (T,λm) = T5 C1
rC5/3 [exp (C2 /C3 )— 1]
It’s included from this relation that the maximum value of radiation intensity surely increases in proportion to temperature to the 5th power. Generally speaking, it is this relation that was obtained by Wien in 1893.
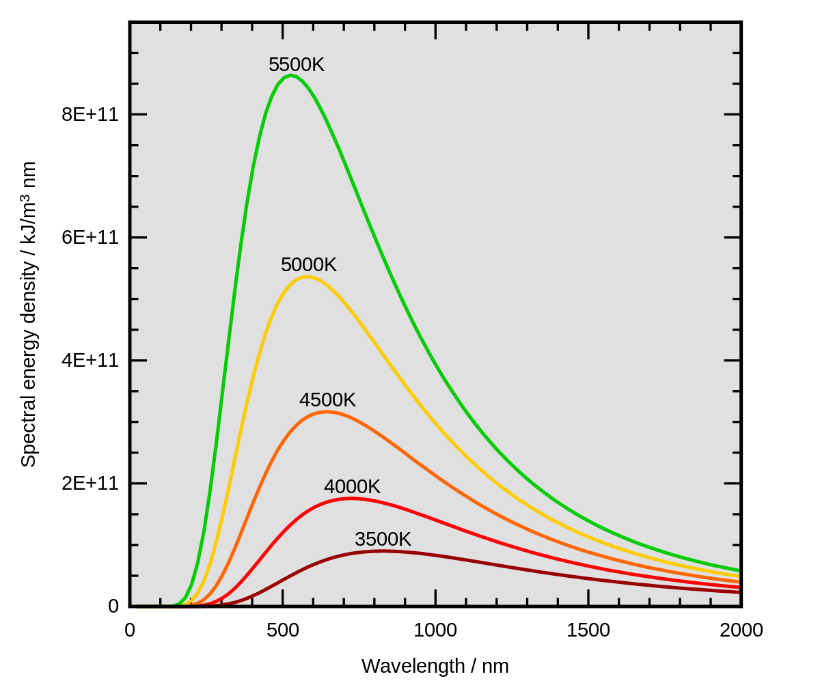
It can easily be seen from the expression that the maximum spectral intensity of the microwave background of the universe at radiation temperature of2.73 H will be approximately equal to 1 mm.